第十五回　三相誘導モータの場合

籠型ロータを使う電磁誘導の仕組みによって電気‐機械エネルギー変換がしっかりとなされるのが，3相交流を使う回転磁界型モータです。前回の隈取（くまど）り線輪モータそれ自体と関連説明で引用した６コイル集中巻きとの大きな違いが分布巻きと呼ばれる複雑な巻線にあります。空隙の1周に現れるＮ極とＳ極の数を極数と呼びます。その最小が2で，巻線の方式によって4, 6, 8…の偶数が可能です。磁界の回転速度は周波数をとすると2極巻線では毎秒回であり，4極では/2, そして6極では / 3です。

図15-1の写真は卓上での実験用に設計された三相籠型誘導モータです。ステータの巻線は4極磁界を形成するように配置と結線がされています。

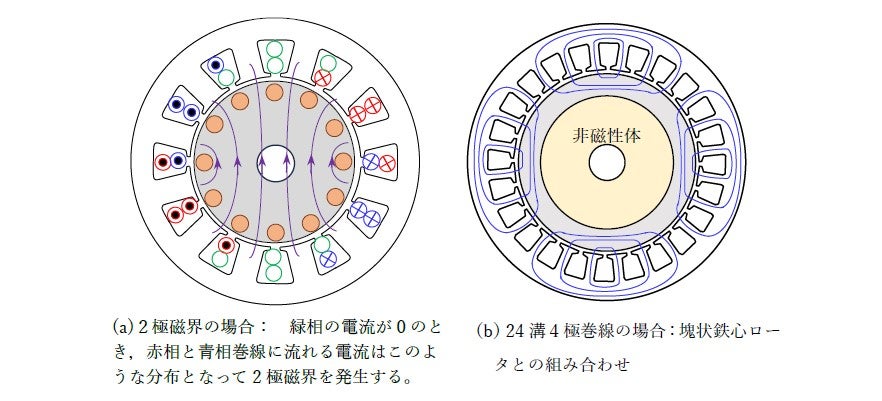
図15-2には回転磁界の意味を描いています。(a)は2極磁界が回転するものです。（b）は24個のコイルを使う4極回転磁界です。コイルを多数使う理由は電磁誘導ができるだけ効果的に発して時間・空間的に滑らかな回転磁界を形成するためです。

籠型誘導モータは，優秀な頭脳によって多くの研究がされました。各部分の構造や使用材料とトルクや電流などの関係も研究されました。計算機がない時代の成果の一つとして等価回路という解析・計算の手法が考案されました。その基になったのがトランスの等価回路ですが，モータ内の鉄心に磁束が通って，コイルに流れる電流との間に電磁誘導現象が起きて，しかも動力が発生するメカニズムの計算ツールです。ここでは，磁場や磁束のことを忘れて，電気回路として電圧と電流だけの仕掛けとして電気回路として計算できるという意味での「等価」です。等価回路の英語は equivalent circuit ですがドイツ語ではEinsatzkreisともいいます。Einsatzには代わりに使えるもの(replaceable)というニュアンスがあるようです。

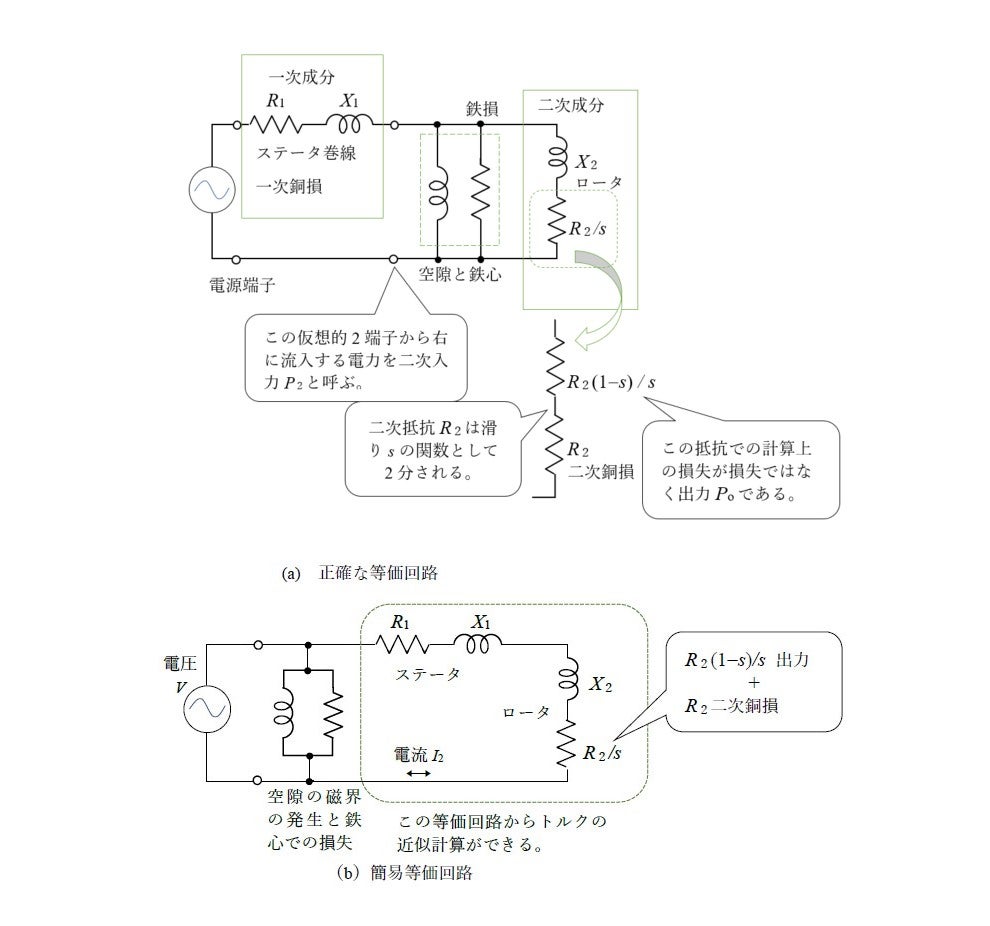
図15-3 に示すのは代表的な2つの回路表現です。(a)では左側がステータ巻線を表し，右側がロータです。中央の（抵抗とインダクタンスの並列回路）は空隙と（双方の）鉄心の性質を表します。右のロータ部分の抵抗値にはという変数がついています。これが回転速度を表す変数です。その定義は：

であり，すべり（slip）呼ばれます。磁界の回転速度（同期速度）とのすべり（ずれ）です。モータの回転速度0は ＝ 1であり，同期速度は ＝ 0です。等価回路(a)はこのように物理的意味をうまく織り込んでいます。 同図(b)は物理的な意味を少し犠牲にした回路です。これによると巻線とロータで消費される電力，そしてロータが発生する出力やトルクが容易に計算されます。

重要なことが以下の計算結果です：

１）回転しているロータの抵抗成分は で表される。

２）電流を とすると， がシャフトから得られる動力(＝出力 ）である。

３）ロータ内の損失は:

４)　トルク と出力の関係：

５）そして

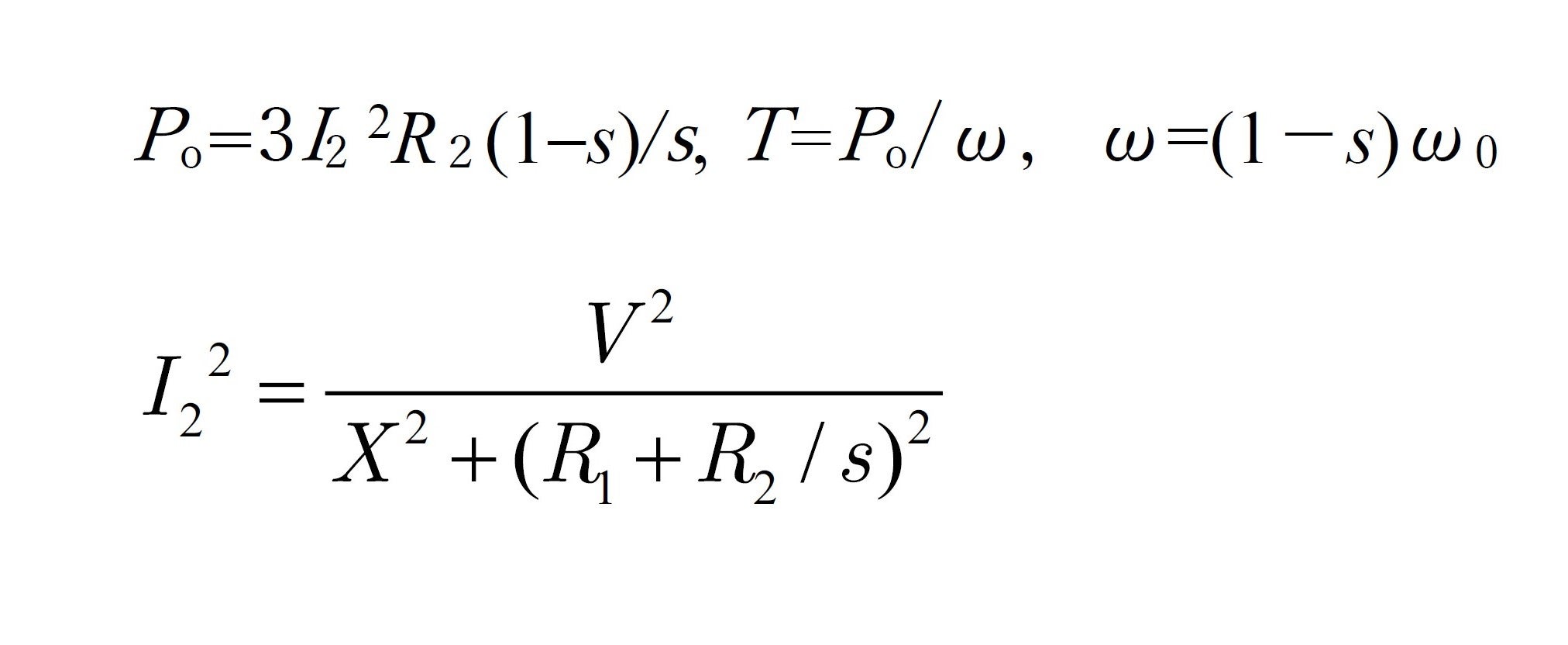
より

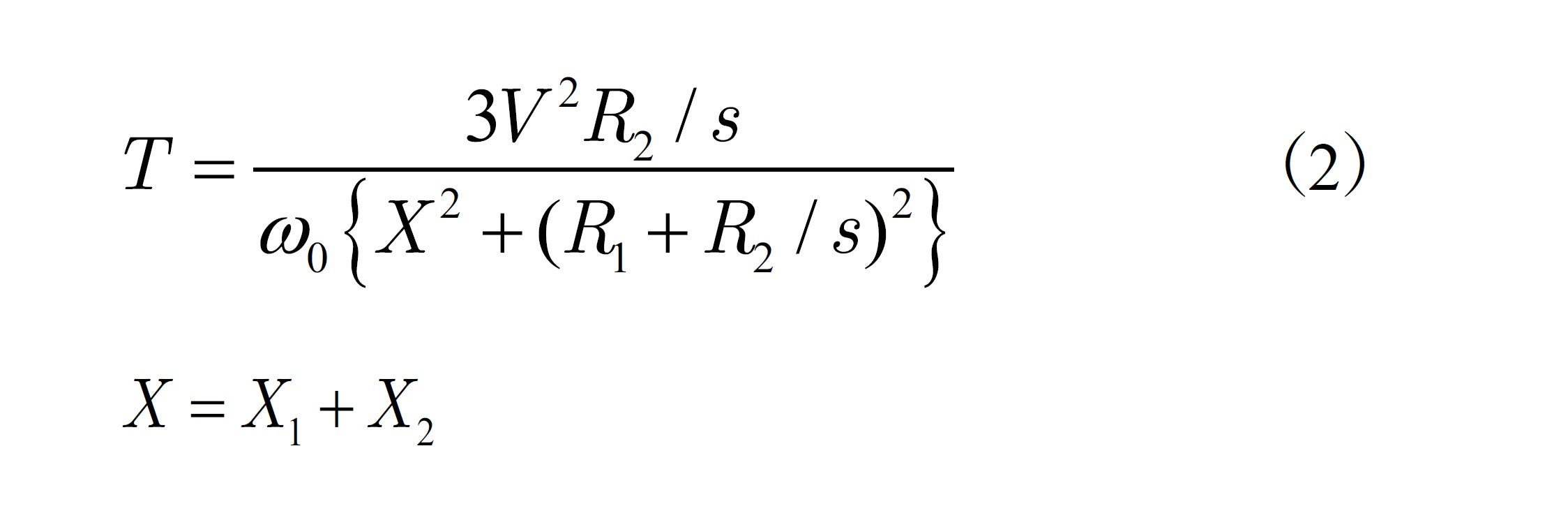
このようにトルク は の関数になり, 使用する導体と寸法によって決まる電気抵抗にも密接に関係します。それを描いているのが図15-4のグラフです。

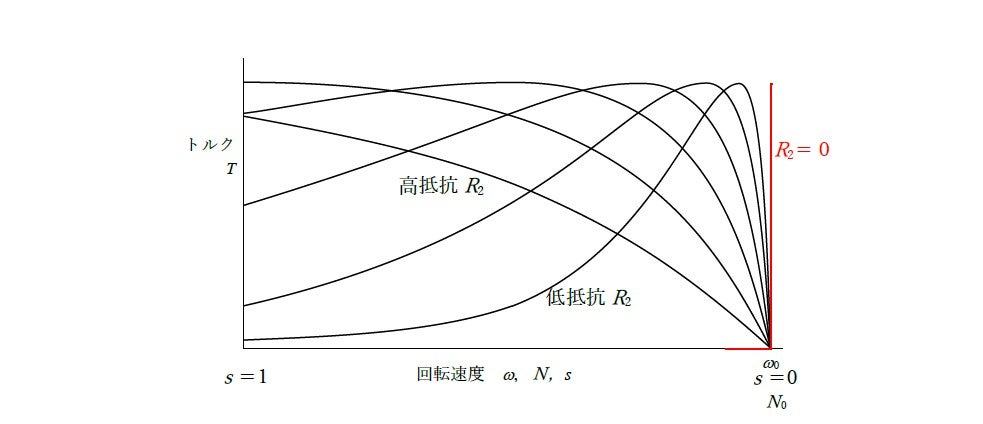
◇ 起動するときのトルクを大きくしたい機種では導体を細くするか黄銅のような合金を使います。この設計では速度と共にトルクが下がるので出力（）は大きくなりません。

◇ 導体と短絡環に銅を使うか，ダイカストによって太いアルミにすると起動トルクは低いのですが，高速でトルクが大きくなり出力が大きく効率（機械的出力/電気的入力）が高くなります。

◇ 産業用の汎用モータでは導体の断面を工夫して全体のトルク特性が調整されています。

上の（2）式に示唆されるように，二次導体の抵抗を限りなくゼロに近づけると赤線のようになります。超電導とは0抵抗のことですから，誘導機としては理論的にはトルクが発生しないことになりそうです。本当にそうだろうか？　次回ではこれが大きな論点の一つです。

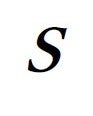＝ 0ではどうなのかの問題も残っています。電磁誘導が起きるためには磁界が回る速度とロータの速度の間にすべりが必要でした。ロータの速度が磁界の速度と同じになったときにはどうなるのでしょうか？問題点はこれです。ロータには起電力が発生しないので，常電導では電流は流れません。しかし，超電導状態では電流が流れ続けることが可能です。この状態はもはや誘導機ではなく同期機です。超電導モータを技術の問題として語るためには，同期モータの種類と誘導機の関係など遊び心で見ておくのがよろしいと思います。それを第16回のテーマにします。そしてまた，モータの奥深い不思議を見るために，電磁誘導とは異なる磁気誘発のことと，第11回で論じた非ローレンツ力の問題に立ち返ります。複雑な磁気現象が簡単な等価電気回路に変身する不思議を語ろうと思います。