モータの不思議と更なる可能性の探究
第十四回 誘導モータの不思議
トランス（変圧器）のモデルから考える
前回（第13回）では誘導子型モータ(inductor motor)の解説をしました。今回は誘導モータ（induction motor）の番です。誘導モータは産業用のモータの中で最もたくさん使われているモータです。超電導を使ってこのモータの新しい可能性を探求されている研究者の一人が京都大学の中村武恒教授です。教授に登場していただく準備として，誘導モータの構造とその不思議を語ってみたいと思います。
電磁誘導の利用： トランスからモータへ
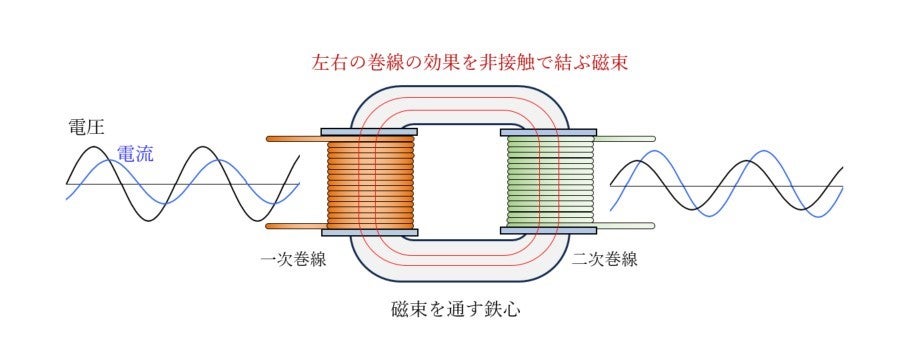
誘導とはいったい何か?から始めます。それは電磁誘導（electromagnetic induction）です。これをトランス(変圧器，transformer)というもので復習します。これは交流の電圧と電流を変換する装置であり，基本的な構造は図14-1のようなものです。たとえば，100Vの交流を20Vの交流に変えるときには，一次側の巻線と二次側の巻線の巻き数の比率を5対1にします。二次側に例えば電球が接続されていて１Aの電流が流れているとします。すると一次側には0.2Aの電流が流れています。一次側の電力は100×0.2＝20Wであり，二次側では20×1＝20Wです。このように(理想的に)入力電力と出力電力は同じです。
隈取り線輪モータ
変圧器は電力を電力に変換する装置ですが，これに工夫を凝(こ)らして電力を動力に変換する仕組み（モータ）ができないでしょうか？ 動力の定義は回転速度×回転力（トルク）です。つまり
（電圧×電流） （トルク×速度）
を司る仕組みのことです。これは電気力学（Electrodynamics）の基本的テーマの一つです。
そのような装置の典型が図14-2の隈取(くまど)り線輪(せんりん)モータです。図14-3の写真ではロータ（回転部分）の構造が見えます。３か所に短絡メカニズムを構成しています。一つはロータ自体の籠(かご)型導体です。そしてステータ鉄心が狭くなる隈部分（すみ）に設置された2個の線輪（一巻のコイル）です。
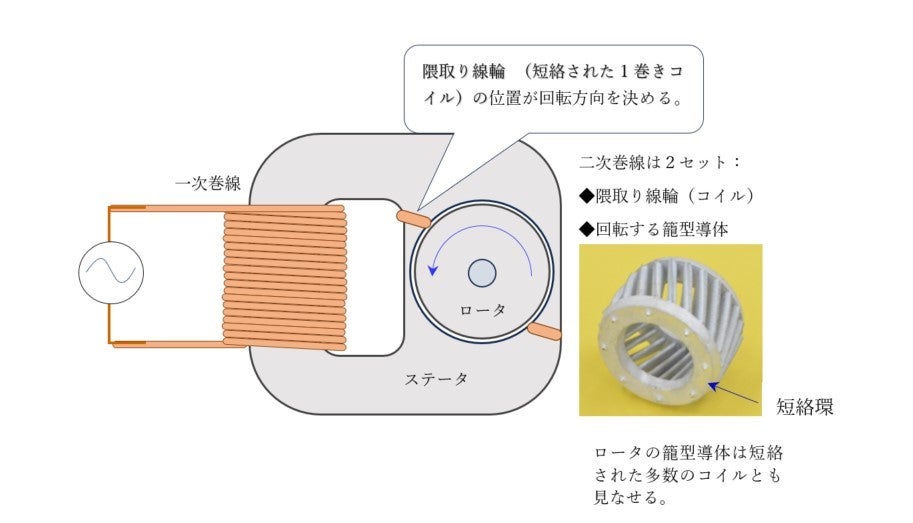
隈とは何か，ある辞書によると「奥まってかくれたところ。すみ」であり「隈取り」は「日本画で遠近感をだすために絵具をぼかすこと」とあります。 動詞のto shade を遮ると理解します。何を遮るのか？ この問いに答えるのは容易ではありません。そこで少し回り路をします。隈取り線輪が無いとどんなことになるのかの問いからです。永久磁石を使うモータの研究歴ほぼ10年のW君に問うてみました。すると『モータにはならないと思います』ということでした。
この問答に始まる実験は，モータの設計や制御に自信をもっている研究者をぎくりさせることになるかもしれません。後日，筆者はある段取りをしてからW君を含めて3人の若い研究員とともにさまざまの実験を行いました。その一部を説明します。使った機材はMechatroLabです。3タイプのステータと種々のロータを備えたこの卓上実験機はさまざまの現象を見せてくれます。
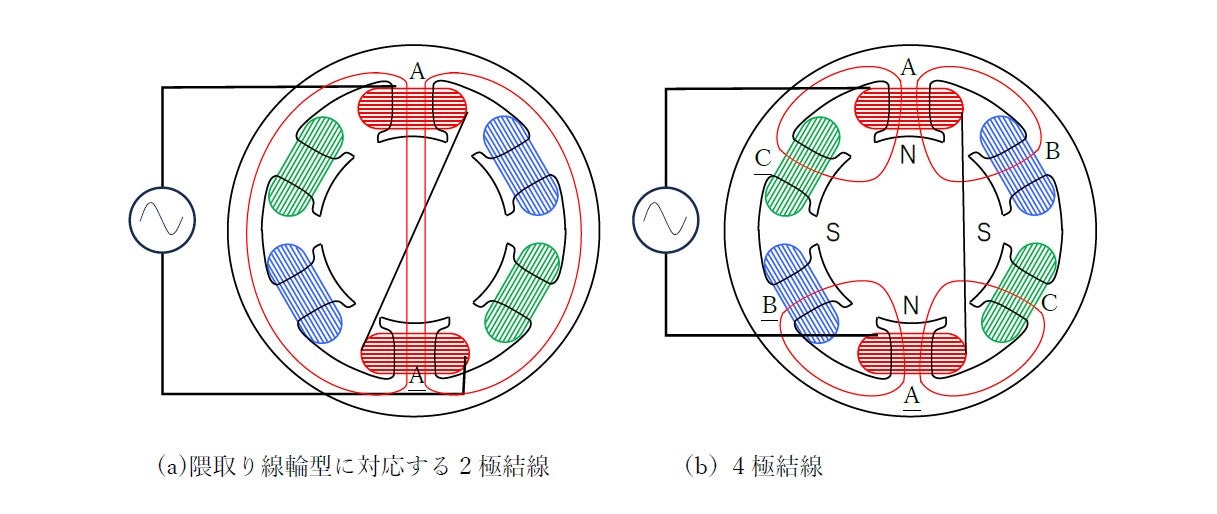
ロータとしては図14-4に見る2タイプを使います。左の籠型と右の塊状鉄心型です。この写真ではコイルを６個備えたステータに籠型ロータを設置した状態を見ています。この６個のコイルの意味を説明するのが図14-5です。コイルに名前をつけてA,A, B,B, C,Cとします。まずAとAを直列に結線してこれに50Hzの交流電圧を印加します。このときの結線法が2つあります。直流の電流を流したときの磁極が異極（NSあるいはSN）になる結線と同極（NNあるいはSS）になる結線です。その違いを示すのが図14－5(a)（b）です。異極結線のときにはAAは2極磁界を発生し，隈取りモータの磁界に対応します。図（b）は同極結線の場合であり，4極磁界になります。電流の無いBBとCCの歯が磁路を提供しています。写真図14－4の結線はこの場合です。
対称性とその破れ
この見出しは最先端物理学を匂わせます。アインシュタインは単極発電機での対称性の要請からローレンツ変換を導き，特殊相対性理論―運動物体の電気力学―を提唱したのは1905年でした。第12回のテーマはこれでした。2008年のノーベル物理学賞は，大宇宙が存在する理由に関する対称性の破れをテーマとして，南部・小林・益川に授与されました。
対称性（symmetry）と非対称（asymmetry）をモータの科学に持ち込んでみましょう。
まず，ステータは異極（2極）結線にして，ブラケットをかぶせ，ロータがさらさらと回るようにしてから，電圧を少しずつ上げてみたのですが，ロータは静止したままです。動きません。W君が思ったようにモータにはなりません。ひょっとすると，彼の頭脳には図14.6 のようなイメージができたのだろうと思います。左右・上下対称な構造と磁界です。この対称性のために，ロータがどちらかに回転する根拠がないように見えます。この意味でW君の答えは正しそうです。しかし，ダランベールの『仮想変位の原理』というものがあります。実際には静止している状態ですが，仮にCWにあるいはCCWに動いている（あるいは変位したら）としたらどうなるのか？これは対称性の破れのチェックです。もう一つの観点として初期条件があります。巻線に電圧を印加するときにロータは静止しているのは初期条件の一例にすぎません。
ここからが筆者の演技です。図14－5(a)の配置で，電圧を上げながらシャフトを2本の指でつまんでＣＷ（時計方向）に回して指を放したところ，ロータはその向に加速してモータとしての動きを見せてくれました。その動きを指で止めてから，今度はCCWに回したところ，その方向に加速しました。この実験は3人に研究員とっては始めて知った単相籠型モ―タの原理の実演です。指で回したことは，初期条件の変更です。
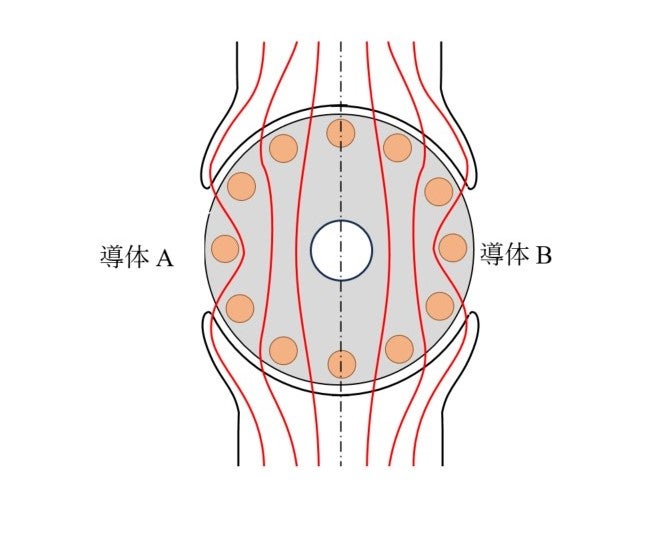
図14-6 左右上下対称の静止状態に左右対称の交番磁界をかけるとどうなるだろうか？全磁束を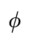
とする。導体AとBは短絡されている。そこを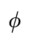が通過して逆起電力 
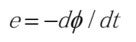が発生して電流が流れ，それによって新しい磁場が生まれるのだが，交番磁界であるから，時間的に平均すると0になるので運動（回転）は起きないと思いこむかもしれない。初期条件としてCWあるいはCCWに僅かでも回転しているときには対称性が敗れる。どうなるのだろうか？ベアリングによる制動力がない状況で計算したり考察したりしたい。
不安定から安定へ
数学を使う電気力学は紙上で展開されます。初期条件としてCWあるいはCCWの僅かの速度を設定して，導体が磁界を切って発生する起電力とそれによる電流の式を求めて，基(もと)の磁界との相互作用として動きを加速する力が導体に作用することが導きだされるかもしれません。理論的思考では紙上の計算に納得するかしないかの問題点が残ります。指を使った上の実験はこの疑問を残しません。この実験から分かったのが図14-6は不安定な対称であり，外力が加わるとその方向に動きだす状況です。動き出し，加速するのですが，ある安定した速度に落ち着きます。これは単相籠型誘導モータの特性です。
次に，ロータを図14-4 右）の塊状鉄心型ロータに差しかえてみました。指で手伝っても加速することなく止まってしまいました。これは安定な対称です。この2つのタイプのロータに現れる不安定と安定の違いを的確に理論的に把握して説明するのは容易ではないと思います。
次に，再び籠型ロータに差し替えてステータの結線を4極磁界にしてみました。そして同じような現象を観測しました。籠型ロータの大きな特長としてどんな極数のステータにも対応できそうです。
短絡線輪の意味は何だろうか？
ここでふたたび図14-4の結線を見てほしいのです。BとBそれぞれのコイル（巻線）をばななジャックのリード線で短絡してみたのです。すると自起動したのです。向きはCCWです。次にBBに代えてCCを短絡したところＣＷに回り出しました。図14-3のような隈取り線輪の場合とは反対向きです。ここにも誘導モータの不思議が垣間見られたと言えそうです。
隈取り線輪を取り外しても自起動！
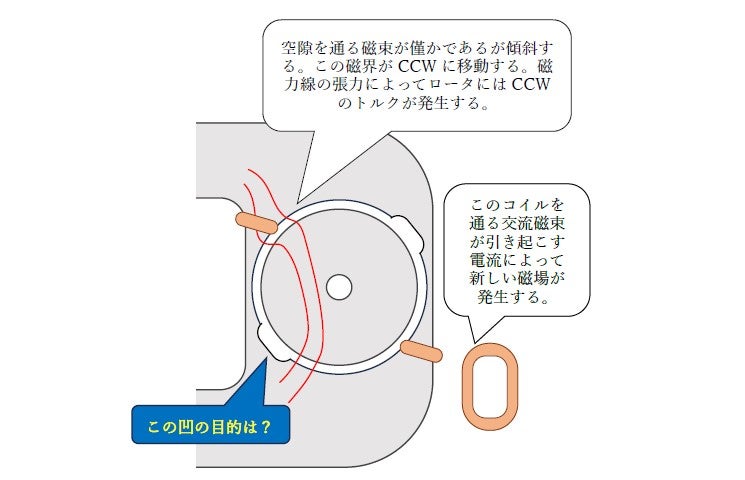
いよいよ，隈取りモータでの実験です。図14-7はこのモータの仕組みの要点を描いたものです。隈取り線輪は明らかに非対称を構成しているので，これがロータを起動させることが納得できそうですし，教科書やWEBにもそれらしい説明が掲載されています。
次に，図14-8の写真のように隈取り線輪を切断・除去してから電圧を印加して上げていきました。結果は：
- 低い電圧（線輪があるときに起動する電圧）では回り出しませんし，指で手伝っても加速しません。
- 電圧を引き上げて所定の100Vに近づくと回り出しました。線輪があったときと同じ方向です。
トルクに関する理論的な考察においては，前提条件や，面積分と体積積分に関するガウスの定理の導入，境界条件などの首尾一貫性に注意しなくてはなりません。それを語ろうというのは本稿の目的ではありませんが，一つだけ注意したいのが作用・反作用の原理です。空隙を境にロータ内の電磁現象で計算されるトルクは，この原理によって，ステータ内で計算されるトルクの逆になるはずです。英国のエンジニアから聞いたことですが，電磁学の発展史で，作用・反作用の原理に疑問が発生し，それを克服しながら今日のマクスウェルの理論と呼ばれる体系が整備されたようです。
ここで，この原理を持ち出すと”何か変だな”と感じます。ロータ内には導体があって電磁誘導によって電流が流れその周辺には磁界があるのでトルクの発生は説明できるかもしれなません。しかしステータの鉄心には電流もなく，線輪もないのでトルクが発生するようには思えないのです。つまり，ロータに対する反作用が無さそうです。ではどのように釈明して理論づければよいのでしょうか？その答えは図14-7に指摘している凹構造にあって，前回論じた非ローレンツ力であり，B‐H平面での幾何的な計算を根拠にできるだろうと思います。 ちなみに，1940年にAIEE誌に掲載されたTeareのヒステリシスによるトルク式（非ローレンツ力の一つ）の導出は分かりやすい論理です。その3年前にYale大学に提出された学位論文では小ループを含む複雑な非線形の問題を彼は仮想変位から論じていました。
次回は，産業用として広く普及している三相交流を使う籠型誘導モータを取りあげてみましょう。
