モータの不思議と更なる可能性の探究
第十二回 ジーメンスのUnipolarmaschinenの電磁界から導かれる相対性理論
前回に引き続いて，非ローレンツ力と相対性理論について考察してみようと思います。モータの電気力学と相対性理論は，大学工学部のカリキュラムに組み込まれるのが自然であると思います。それを論じてみます。
この根本を考えたのがアインシュタインです。マクスウェルが光は電磁波であることを主張し始めたのが1864 年ごろでした。これが相対性理論の伏線でもありました。1905 年にアインシュタインは画期的な論文を5 編も著したのですが，2 編が特殊相対論に関する彼の発想です。最初の『運動物体の電気力学』には括弧付きで（Unipolarmaschinen）が１回だけ現れます（図1）。ここれが本稿の枕詞でもあり，筆者の疑問でもありました。
技術的装置で考える哲学者
ずっと後にアインシュタインはある知人への手紙に，「私は理論物理学者である思われているが，自分ではむしろ哲学者であると思っている。そして新しい理論を考えるときにはいつも技術的な装置を考えた」としたためています。そしてジーメンスのUnipolarmaschinen が特殊相対論のヒントであったと述べていたのです。図2はこの疑問を解き明かすために制作した機材であり，図3はその説明図です。
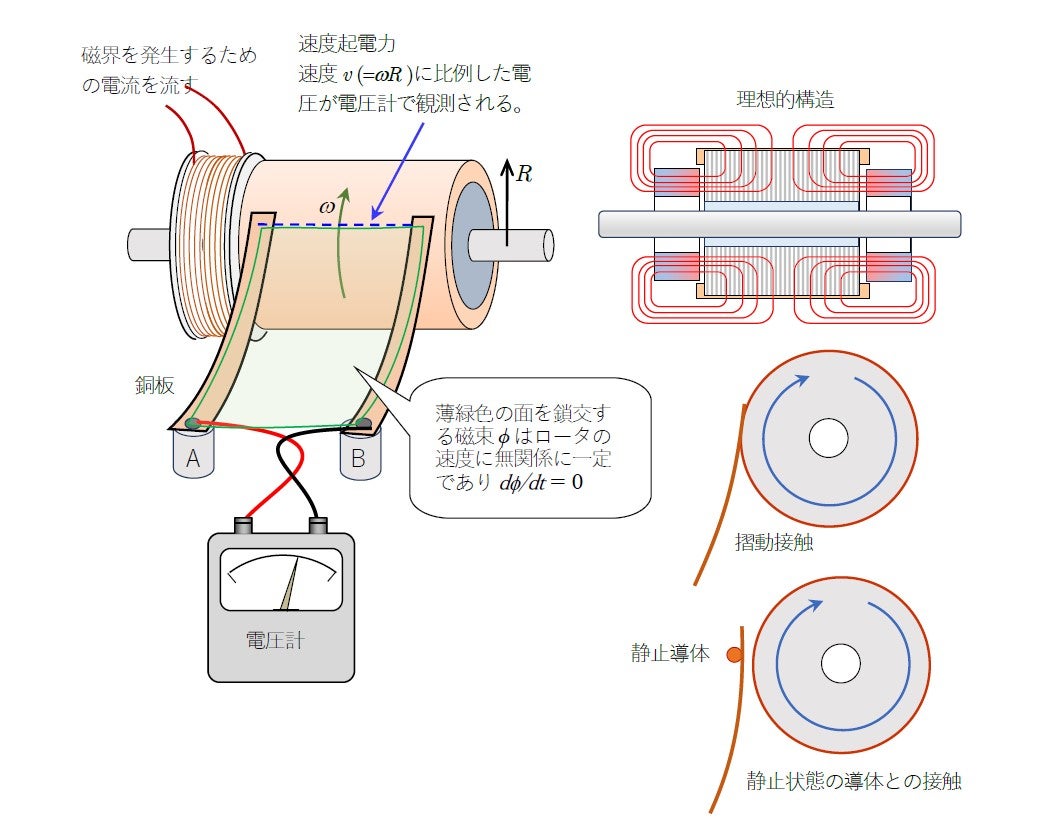
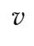に比例する 速度起電力が静止系で計測される。 2 枚の銅板を接触面から離して静止導体に接触させると電圧は観測されない。今回はここで，ニデックのある研究員を紹介してみようと思います。大学では航空宇宙を含む機械工学を専攻し，修士課程を修了し，20 11 年入社の研究員です。T 君とします。2022年10 月に佐野茂氏と『一般相対性理論』[1]を技術評論社から出したときに早速読後感を書いてくださいました。Ｔ君の的確なコメントの一部を紹介します。その中に，第8 章で「特殊相対性理論があまりにあっさり導かれることに驚いた。」とあります。この部分はドイツ語による込み入った論理の解読は困難と悟って独自に導いたものです。T 君は第9 章での一般相対性理論の根底に関するドイツ語の読解が面白かったということです。
一般相対性理論は重力に関係する大宇宙の時空の法則です。これはまさに理論物理ですから技術的な装置とは無縁のように思えます。しかし，等価原理というものを発想させたエレベータが機械的な装置です。当時の欧州ではモ―タを使うエレベータは最先端技術の一つでした。
『一般相対性理論』 T君のご読後感から
大学の講義では相対性理論にはあまり触れませんでした。しかし一般相対性理論に興味があり，豊富でカラフルな図形に助けられ，数式を追って本書を読んでみたというよりも，読めました。また，アインシュタインだけでなく，様々な科学者・技術者が相対性理論の発展に寄与してきたのが物語として分かります。彼らが宇宙の謎を追い求める物語は気持ちをワクワクさせ，難しい理論の理解を助けてくれます。
第1～4章は・・・・（略）
第5章で時間の概念が導入され波動の話がでてきます。大学1年生の化学の講義でいきなり波動関数がでてきて面喰ったのですが，本章では「波動」の意味や取り扱い方が分かりやすく書かれています。
第6章は電磁気学です。相対性理論と電磁気学にどんな関係があるのだろうと訝ったのですが，第8章で相対性理論を思いついたアインシュタインの考察につながります。著者の見城氏はモータの実用化への理論では日本の第一人者であり，難解な概念的な電磁気学と実用的なモータの繋がりがわかり，このような観点で電磁気学を学べるのも良いと思います。
第7章にはアインシュタインが相対性理論を考案する前の子供のころや学生時代の科学史が展開され，相対性理論の発見はどのような歴史的背景で導かれていったのかがわかります。・・・・略
第8章で特殊相対性理論の解説になり，第7章の電磁気学を背景として特殊相対性理論が，あまりにあっさり導かれることに驚きました。・・・・（略）
第9章は一般性相対性理論を導くのですが，ここでも難しい式が前半の幾何の話と結び付けられ，図形的な意味と物理的な意味がつかみやすくなっています。また，アインシュタインのドイツ語を読み解くことで，その奥にある考察を読み解く試みが面白いです。時制の使い方の分析からアインシュタインの深い物理的な考え方に触れることができたと思います。
以下略
電磁モ―タとガリレー変換 ―基本法則の再検討
相対性理論の講義を受けたりあるいは独学した人は，相対性理論といえばローレンツ変換であると早合点するかもしれませんが，ガリレー変換が出発点です。
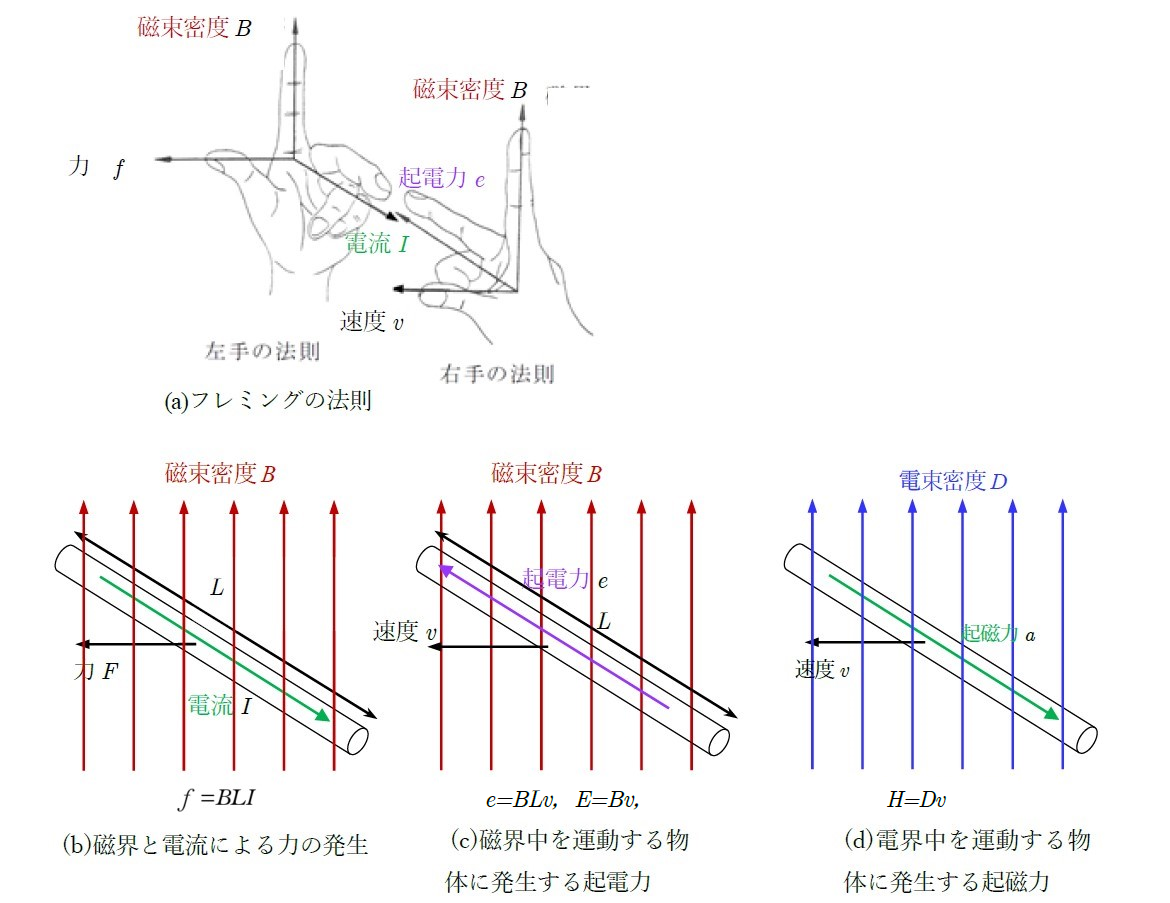
ここで物体の運動と電磁力に関する当たり前のことを図4によって見直します。複雑な関係を分かりやすく説明したのがフレミングであり，左手と右手の関係として図4(a)があります。これはモータと発電機の関係もあります。あるいは電磁力と起電力の関係ともいえます。モータには発電作用が宿されていることは天からの恩恵ともいえます。
相対運動
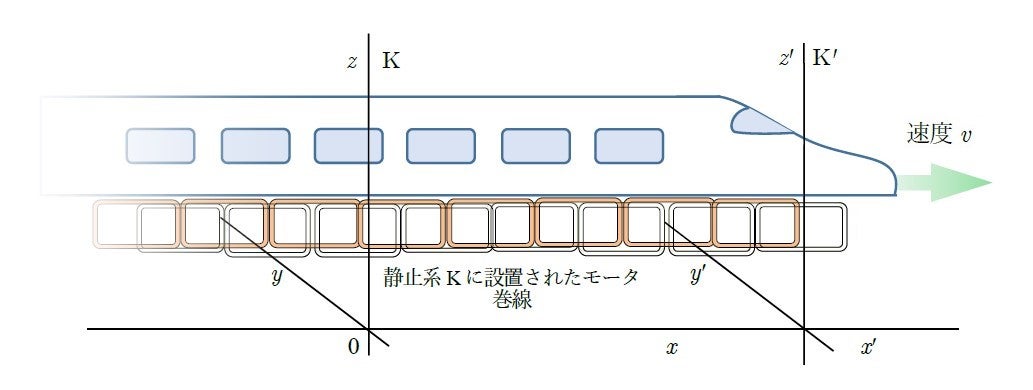
ステータ（固定子）とロータ（回転子）の関係は相対運動の関係にあります。回転型モータに代わって図5のようにリニアモータを想定します。図6ではステータとロータ（走行体）の各々に座標系を設定して，一方が静止系であり，他方を運動系として相対運動の意味を考察する基盤とします。そして次の問答をしてみます。当たり前のようなことが当たり前とは言い難いことが見えてきます。少年Albert Einstein が叔父のJakob Einstein が運営する工場で技術者の間でささやかれていた疑問― 非対称問題 Asymmetrie ―です。
当たり前のことして，原点からの距離 
と時間 
に関して図6に示す2 つの系の間には次の関係があることから始めます。
次に図4にもどってフレミングの右手の法則を調べてみます。磁界 
を切ると電界強度 
が発生し，それぞれのベクトルの向きを示すのが右手です。それが次式になります。
次に相対運動に関する対称性（英symmetry, 独Symmetrie）について考えます。図6の 
は運動系ですが，これと共に運動する観測者にはこれが静止系であり， 
は 
で運動する座標系です。上の2つの式で左右の項の入れ替えをすると次式が得られます。
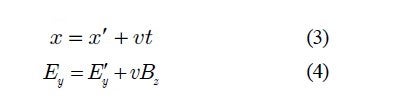
めでたし，相対運動としての対称関係が確認されました。
しかし，これはファラディまでのことです。マクスウェルの登場によって非対称性が現われます。それを解消して新しい対称性を提唱したのがアインシュタインであり，それが特殊相対性理論です。
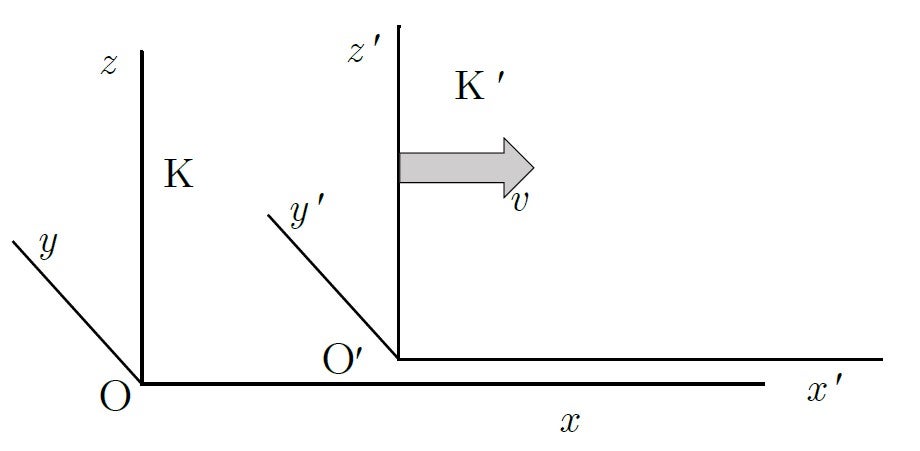
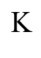の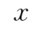 軸方向に速度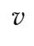で動いている運動系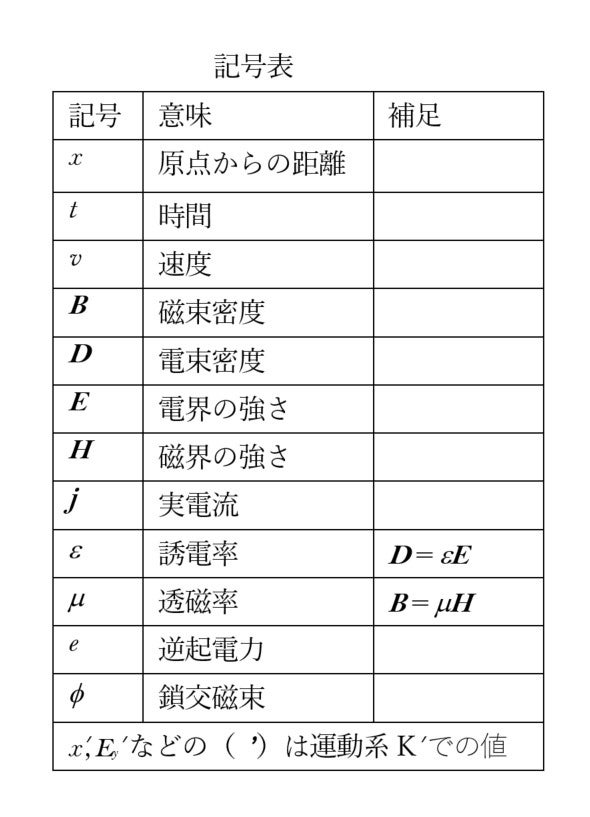
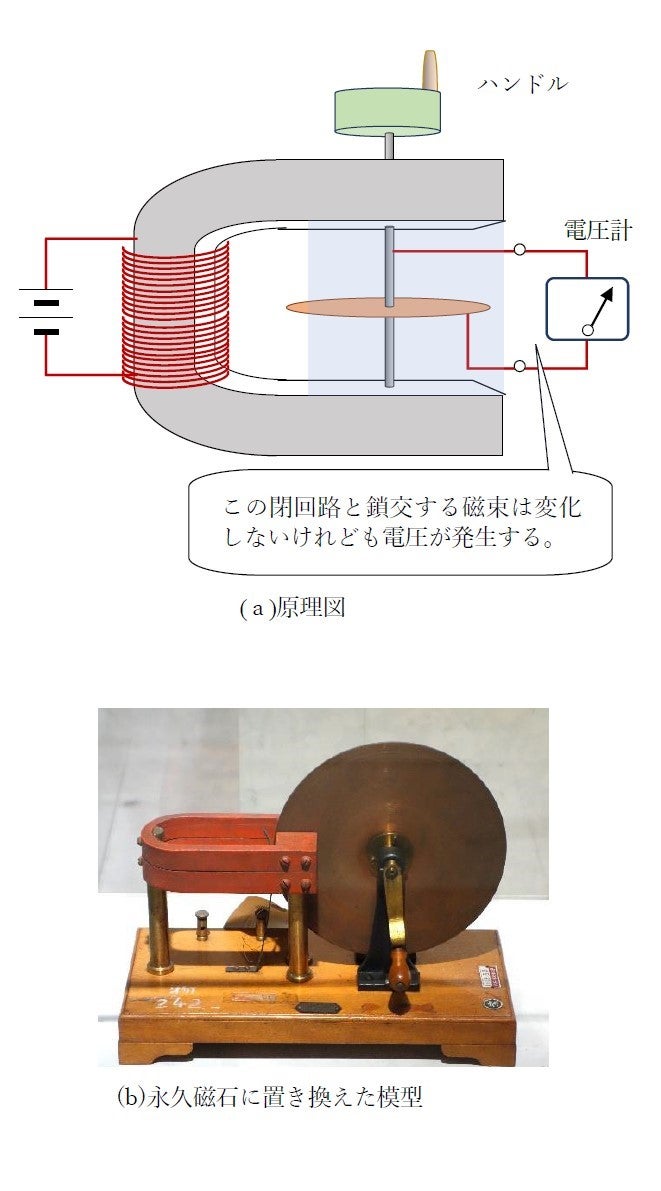
それを語る前にファラディが指摘した重要なことをしっかりと見ておきましょう。図7は1831年に行ったとされる彼の発電機の実験です。今日ではunipolar generatorと呼ばれるのですが，その当時にはその用語はまだ無かったと思います。またそれは，アラゴの円盤の延長として確かめられた実験であると想像されます。そこに示した閉回路だけを見ると円盤の回転に関係なく鎖交磁束 
は一定ですから単なる電磁誘導の法則
だけでは起電力 
の発生がありません。閉回路を構成する要素の中に運動があると磁界を切ることによる起電力が発生します。しかしファラディの場合には，問題とする導体の速度vが軸からの位置によって異なるために数式による理論展開が単純ではありません。アインシュタインの少年時代に，叔父の工場で論じられていたのはジーメンスの単極発電機であり，Unipolarmaschineが技術用語になっていたようです。それは先の図3のようなものであり，運動速度 はどこでも 
です。
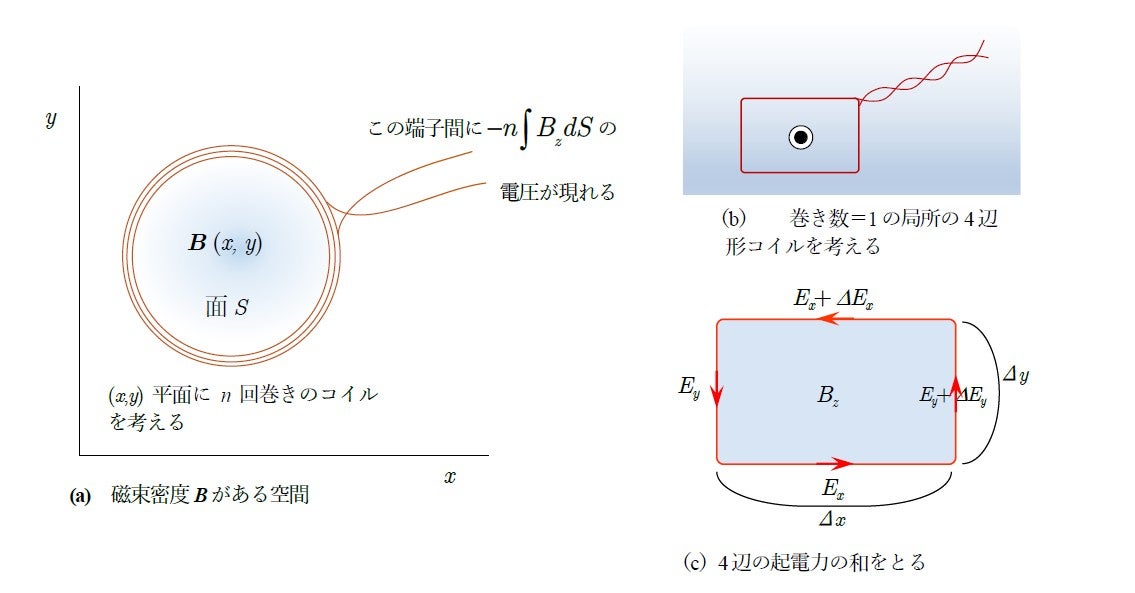
ここで，電磁気学の数学として，2 つの扱い方に関して若干の補足をします。まず，図8で(a), (b), (c)の3 つのコイルを使って示すように，小さな長方形コイルに発生する電磁誘導を適用することによってマクスウェルの方程式の1 つ
を導く方法です。ここでは巻き数＝１の長方形コイルに電磁誘導の原理式（5）を適用すると， コイルに沿う電界 とコイルが囲む磁束の関係は次のようになります。
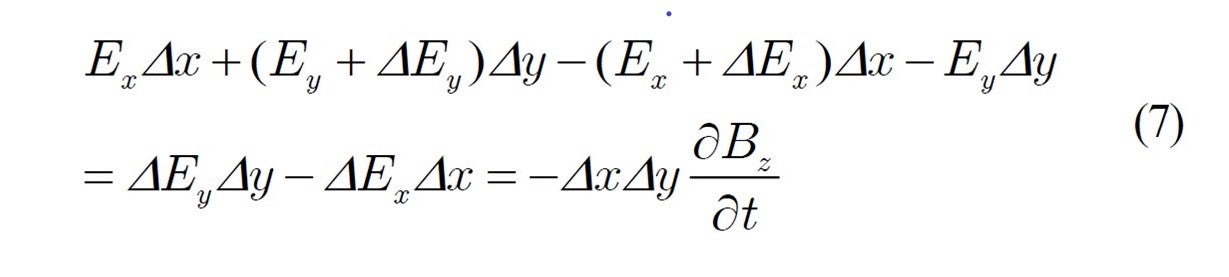
これより
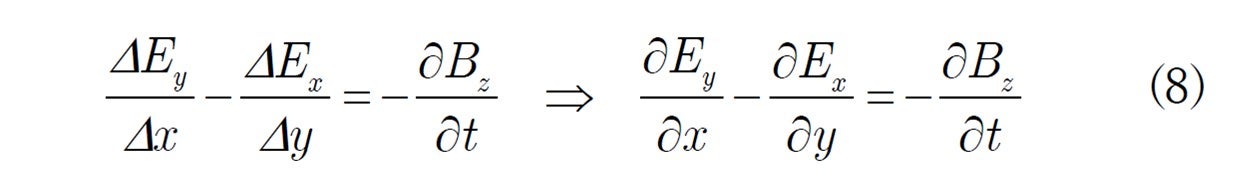
一般化すると上の(6) 式になります。
これは，静止しているコイルの場合でした。次にコイルの一部が運動している場合を図9 のH 型導体と摺動する導体の場合に電磁誘導の原理式(5)を適用します。ここでは磁界も電界も一様です。赤の積分路が囲む面積は時間的に変化しているので鎖交磁束も時間的に変化します。この視察から(2) 式が得られます。これはフレミングの右手の法則でもあります。
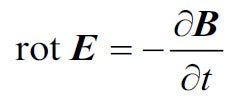が導かれる。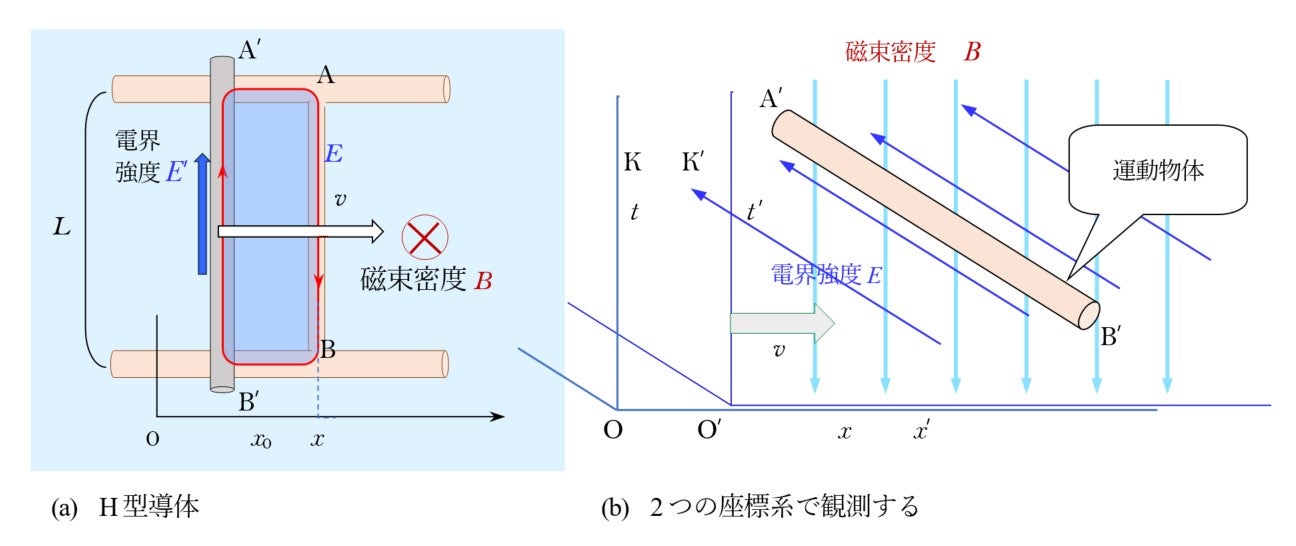
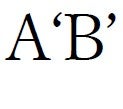を含む閉回路に電磁誘導の法則を適用すると右手の法則
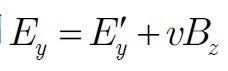が得られる。ローレンツ 変換
アンペアの周回積分定理 
を，(6) 式を得た手順にならって， 
に書き改めることができます。
ファラディの発見と見識を真摯に受けとめたのがスコットランドに誕生したマクスウェル（James Maxwell）であることを読者はご存知かもしれません。磁界 の変化が電界強度を発するのに似て，電界
の時間的な変化が磁界強度
を発生するのではあるまいか？ そのように仮定して，彼がアンペアの式を次のように書きかえたのが1864年とされています。
ただし，このような今日のベクトル解析式に整えたのは後のヘビサイド（Oliver Heaviside）です。
ここで 
は実電流です。実電流とは，電子が真空中や導体の中を運動することによって発生する電流です。それに対して右辺第2項 
を変位電流と呼びます。本質を見るために 
の場合
を考察します。
これは（6）式と類似の形をしているので，連想から次の代数形式が連想されます。
（10）式の右辺には負号（－）が無いので 
ではあるまいかと思うかもしれないのですが，ベクトルの方向成分を考慮すると(11) 式が正しいです。
ここで 
と置いて(4) 式を次式に書き換えます。
(11) , (12) 式を連立させて逆変換すると
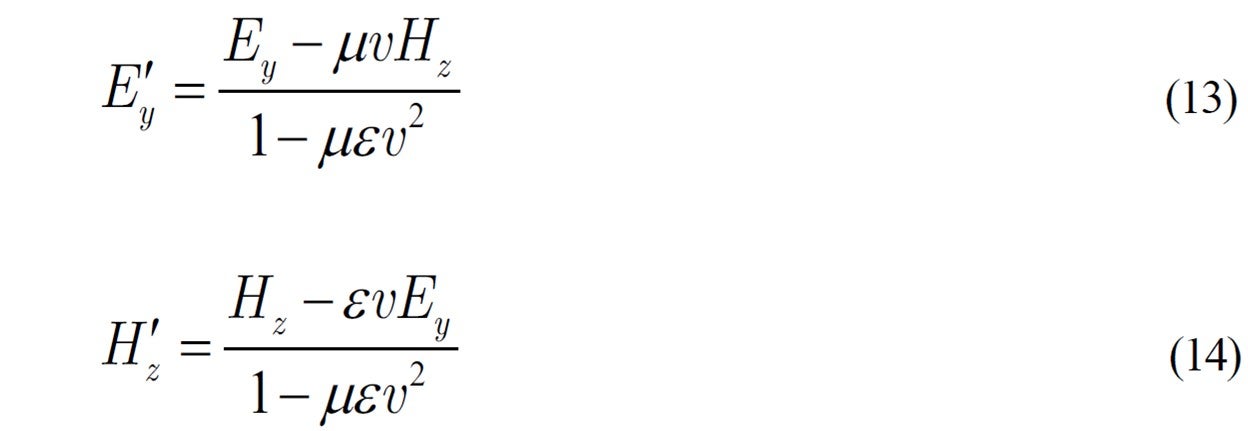
になって，対称性がなくなります。つまり相対性に矛盾が現れます。実際問題としては 
程度ですから 
は1に比べて無視できるので近似としては対称的です。でも理論的に釈然としません。ここが当たり前でないことの始まりです。
非対称性の解消－それが電磁界のローレンツ変換だ！
アインシュタインは，1905年の論文でこの非対称問題を解消したとしているのですが，この論文のごたごたした説明に代わって，行列を使う線形代数学を使ってさらりと解消してみましょう。
先の(13)と(14) 式に代えて 
という係数を導入して次のようにしてみます。簡単のために下付き記号を省きます。
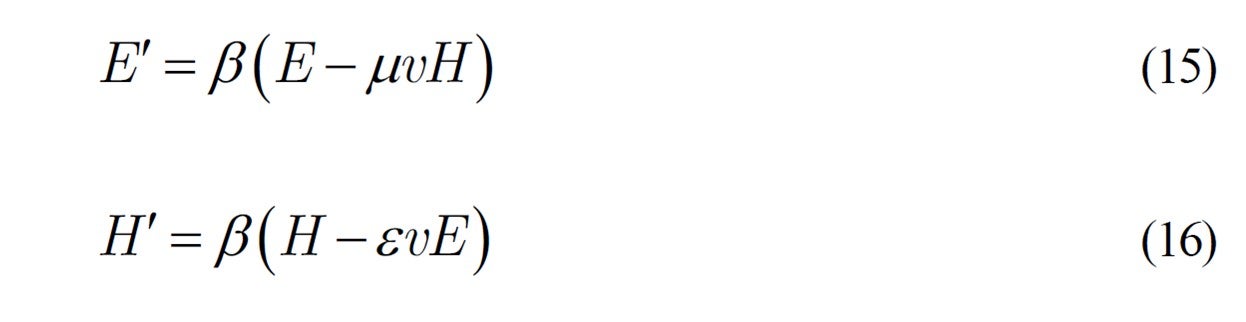
これを1次変換式で行列を使って書き改めてみます：
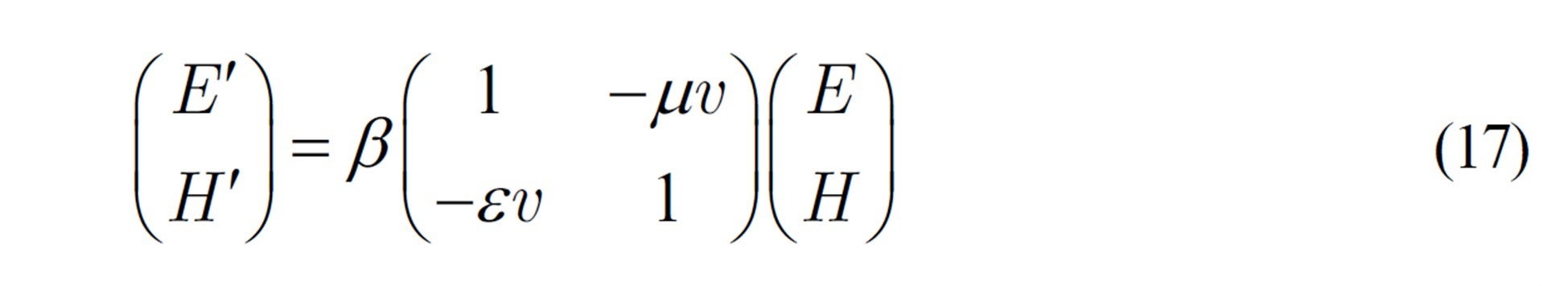
ここで変換行列の行列式は
であり，これを考慮すると上の式は次式になります。
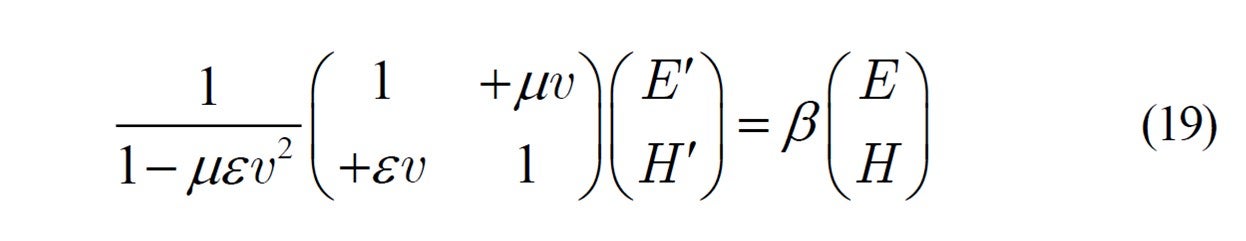
すなわち
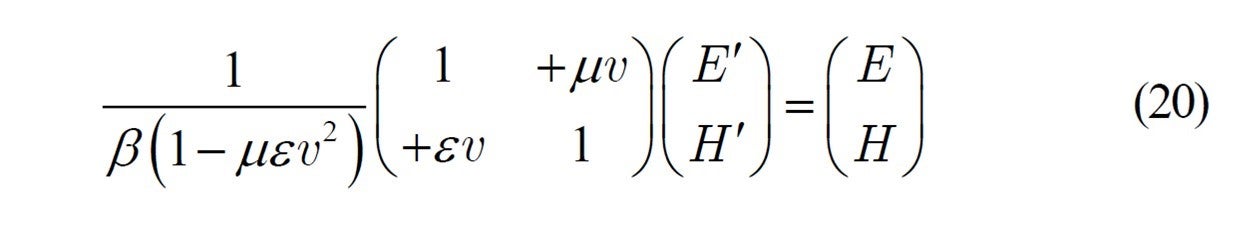
ここで (17) 式において を に変えた対称関係
が成り立つためには，(20) 式との比較から
であればよいわけです。
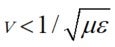の意味を考える
上に得た(22) 式の が実数であるためには 
でなければなりません。これは一体何を意味するのでしょうか？いま考察対象とするロータは銅あるいはアルミ等の金属ですが，透磁率 
と誘電率 
は真空中の 
とほとんど同じです。すると 
は光の速度 
です。そして，
はローレンツが提唱したローレンツ変換の鍵になる要素ではありませんか！
時空のローレンツ変換
さて，マクスウェルの電磁界方程式自体が変更を受けて が入ってくるのでしょうか？ ここが次の考察のステップです。時空に関してもガリレー変換に代わって次のローレンツ変換が成り立つことが予想されます。
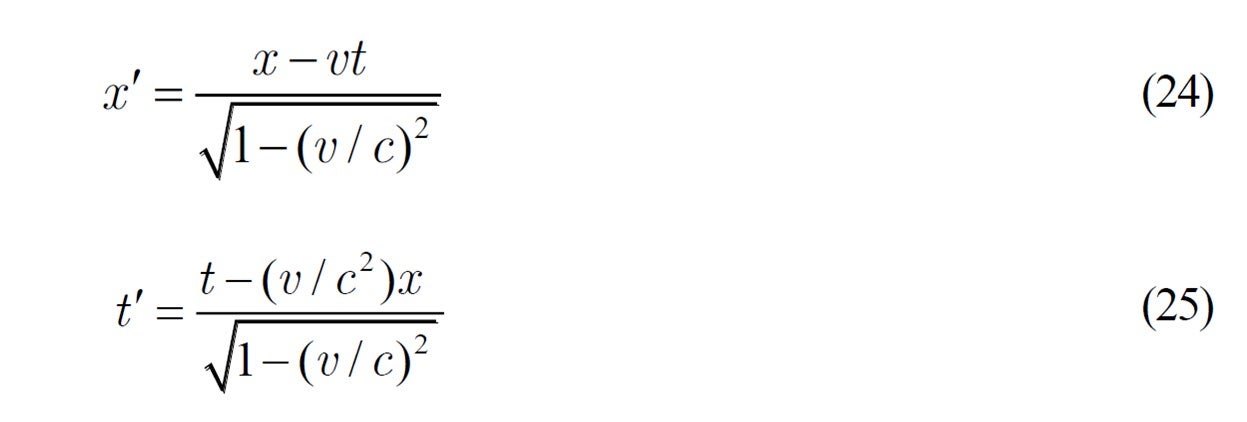
これを見ると， 
とすると運動系の位置 
と時間 
が虚数になります。そして 
では 
になるので非現実的です。したがって相対運動の速度は
でなくてはなりません。つまり，私共が高速宇宙船を設計しても光速 を超えることはできないのです。これは当たり前のことでしょうか？
光速不変の原則
光速 は です。これを構成するパラメターは真空の透磁率 
と誘電率 
です。止まっている真空と動いている真空を区別することはできないとすると，光速は光源の速度に無関係に です。これが限界速度であり，これを超えることはありません。『これを公理として電磁気の理論と力学を統合しよう。』これが若きアインシュタインの電気力学の発想であったと思います。
アインシュタインの理論がすんなりと読者に受け入れられるかどうか？ 納得できないのが自然だと思います。理論物理学に長い伝統をもつ英国のケンブリッジ大学の学派の人々が相対性理論を受け入れるまでの当時（1919年ごろ）の苦難の経緯を研究報告書としたAndrew WarwickのMasters of Theory[2]があります。興味深いのが英国の伝統である実証主義者にとってはアインシュタインのエイヤー（証明するのではなく公理を主張すること）がなかなか受け入られなかったことです。
あとがきに代えて： ―必ずやる，できるまでやるー
「モータには（回生）発電作用が宿されていることは天からの恩恵ともいえます」と書きました。この意味は深いことを実感します。2023 年の初夏のことですが，私は思いがけない連絡を北尾副社長から受けたのです。太陽誘電(株)様がモータが宿す回生発電を有効活用して１充電当たり1000km走行の電動アシスト自転車の開発に成功し，近い将来の実用化に目途をつけたというのです。同社によるこの技術的挑戦は，2009 年に品川区大崎でのME/L(日本電産モータ基礎研究所)にお越しくださった保坂康夫様を激励した筆者の言葉によって，社内の反対の声が大きいなかで，執行役員高木満男様が説得なさって研究開発をし続けたということでした。ここに論じたようにモータと発電機に内在する物理法則は宇宙を貫く相対性原理です。 これはあくまで物理学の領域の事柄です。さらに電池を含む電気化学と生理学として人の運動能力と健康増進の機能，さらには，違和感なく快適に 回生発電させる仕組みの研究によってsustainable society を目指す事業への視野が大きくなりそうです。（次は充電不要な電動アシスト自転車が目標とのことです。）
参考資料
１．見城・佐野：幾何で見える必ずわかる一般相対性理論，技術評論社
２．Andrew Warwick：Masters of Theory, University of Chicago Press
