モータの不思議と更なる可能性の探究
第四回 電磁界のエネルギー流とモータと発電機の不思議
アインシュタインが「運動物体の電気力学」という表題で1905年に発表した理論が、今日知られている特殊相対性理論です。 互いに等速運動する観測系で同じ光を観測すると、その伝搬速度は同じc（=300,000km/s）でも、観測される周波数は異なります。そして物体の長さは観測系によって異なるというのがアインシュタインの理論です。 絶対静止系というものは存在しない、つまりすべての座標系は相対的なのだという理論を彼は導いたのです。
電磁界のエネルギー流とモータや発電機の原理
このような宇宙空間の中での電磁波は光の一種であり、エネルギーを運んでいます。このエネルギーの流れに関する理論を提唱したのが英国のポインティングです。
エネルギー流の密度Pは電界強度Eと磁界強度Hのベクトル積であり、
P =E ×H
だという理論です。
これはアインシュタインの
マックスウェル(James Maxwell)の電磁方程式自体がアインシュタインの理論にかなっているので、それから導かれたポインティングのベクトルは相対性理論には矛盾しないとされていますが、おそらくポインティング自身は相対性理論について深く考察していなかっただろうと思います。
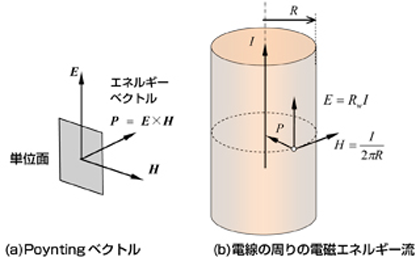
図1はポインティングのエネルギー流の説明で、教科書にもあるものです。これは円形断面をもつ銅線を流れる電流によって銅損が発生することについて2つの説明をしています。
半径Rの電線の周辺の磁界強度Hはアンペールの法則から求められ図示する通りです。電線の単位長さあたりの電気抵抗を
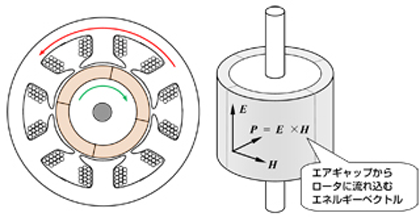
ところが、電線に単に電流を流すだけではなく、磁界あるいは電界の様子に工夫すると、導体(物体)の一部が回転しようとします。この現象をうまく利用しているのがモータです。そこで、さらに深く解析計算をすると、導体でなく磁性体であってもモータができることが分かります。図2は典型的な電磁モータの構造です。ここではステータとロータの間に空隙があることを示しています。
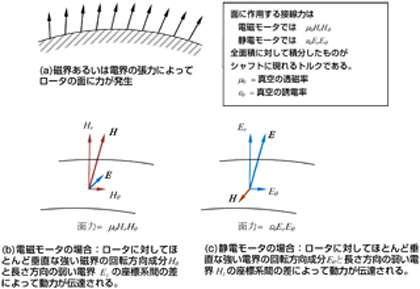
回転しようとするのは、ロータの面に接線力がはたらくからだと解釈できます。これを図3(a)のように磁力線や電気力線の張力として説明するのが、マックスウェルの応力テンソルの考えで、ポインティングのベクトルに結びつけることができます。
図3(b)には磁力線を使うモータを、図3(c)には電気力線を使うモータの場合を示しています。 ポインティングが自分の理論をモータに結び付けようとして思案した形跡はあるのですが成功していません。ポインティングのエネルギー流の速度は座標系によらずに光速cと同じですが、その大きさは座標系によって異なります。2つの座標系の差が真空中を流れる機械的仕事なのです。
この説を提案したのが筆者です。つまり、
(ステータ座標系のPoynting vector）－ (ロータ座標系のPoynting vector）= 動力ベクトル
ということです。
ステータとロータの間には空間があります。これを空隙（エアギャップ）と呼びます。この空隙を電磁エネルギーが通過するのですが、空隙は空気などの気体によって満たされているものの、真空の性質をもっています。 ここでは、さらに考えを進めて、真空は機械的な仕事の源泉である動力を伝搬するというものです。相対性理論では、座標系によって光速cは不変ですが、単位時間あたりのエネルギー流には違いがあって、座標系間の観測値の差が動力だと解釈できます。回転機はこの動力が正であればモータになり負であれば発電機です。現在の水力や風力発電機はこの理論を利用しているともいえます。
狭い空隙の事例を考える
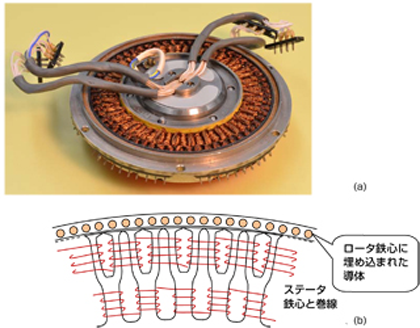
ロータの鉄心とステータの鉄心のあいだの空隙（エアギャップ）は短くてもよく、基本的には機械的に接触しない限り短いことが望ましいです。理由は短いほど空隙の磁界が強くなり伝達する動力密度が上がるからです。図4(a)の写真は極めて特殊な籠型誘導モータで、空隙は通常のモータの1/10ほどです。このモータがどのように特殊なのかというと、
籠型誘導モータでは、空隙をあまりに狭くするとスロットによる空隙磁束の脈動によって損失(漂遊負荷損)が発生するのですが、このモータではステータ・ロータともに極めて細密複雑な工作によって漂遊負荷損を減らすことができるので、空隙を狭くしています。
しかし、電気モータには空隙をさらに減らして潤滑油によって滑らかに回転をさせるようなものはありません。これが内燃機関との違いです。
空隙の長短を利用するSRモータと今後の課題
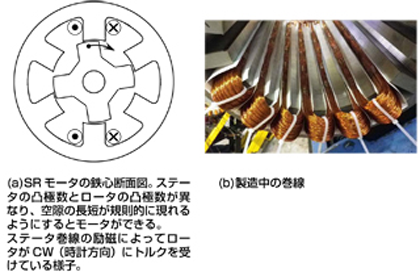
ギャップの長短を利用してトルクを発生するのがスイッチド・リラクタンスモータ(switched reluctance motor)です。鉄心の断面と巻線の様子は図5のようなものです。
これは先の特殊誘導モータとは対照的に構造が極めて単純ですが、駆動・制御するためのエレクトロニクス回路とシステムは複雑です。このモータについては考察する価値があると思います。
永久磁石を使う回転機がモータにも発電機にもなることは容易に想像できると思います。では永久磁石を使わない回転機が発電機なるかどうかはどうでしょうか。 ブラシと整流子を使う方式では自励式発電機というのがあるのですが、これは鉄心の残留磁気をうまく使うものです。
籠型誘導モータは送配電系統に接続されていれば発電機として使うことができますが、単独では発電機になりません。 SRモータは永久磁石も整流子も使わないで単独発電できる珍しい構造です。英国のNidec SR Drivesでは様々な試作と開発を古くよりしています。この可能性をさらに追究するのは必要なことですが、モータ構造のシンプルさに対して、駆動および制御システムは複雑で人工知能が必要です。これが技術的な新しい課題です。
リニア新幹線の物理学的な意味
電磁モータの科学的な意義がいかに大きなものなのかはリニア新幹線が物語っています。地球という座標系と車両という座標系の相対速度が大きいほど、空隙を通って運ばれる機械的な動力を大きくすることができます。
リニア新幹線では磁界の反発力によって車体を浮上させながら駆動力をはたらかせて車体を高速疾走させます。
空隙のないモータ
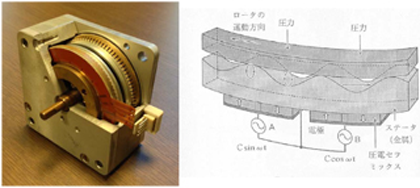
原則を強調しておきながら例外があることを述べるのはおかしなことですが、超音波モータは空隙が必要ありません。超音波モータは指田年生氏の発明によるもので、それは図6の写真と図式でみるように圧電セラミックスがロータ面と接触し摩擦力によって回るモータです。
超音波モータは電磁モータが使えない状況で使えるという意味で、モーションコントロール技術の分野では補完的な役割を演じる重要なモータです。次回でも超音波モータの意味について論じてみたいと思います。
(John Poynting 1852-1914)
マンチェスター生まれ。ケンブリッジ大学の物理数学で優秀な成績を示し、1870年代後半は、カベンディッシュ研究所のマックスウェルのもとで電磁気学を研究をした。
1880年から現在のバーミンガム大学の物理学の教授を務め、エネルギー流の理論を最初に発表したのは1884年である。
その後、光の照射による圧力と接線力の研究を行った。ノーベル物理学者のJ.J.Thomsonと著わした大作A Text-book of Physicsが出版された年に世を去った。
なぜか今では、マンチェスターでもこの偉大な物理学者のことを知る人は少ない。
