モータの不思議と更なる可能性の探究
第三回 相対性理論に潜むモータの不思議
前回までにニコラ・テスラ、シュタインメッツという偉大な人物のことを書いてきました。そこにはシュタインメッツをアインシュタインが訪ねたときの写真を掲載しましたが、今回はアインシュタインとモータの不思議を交えて書いてみたいと思います。
NIDEC中央モータ基礎研究所の玄関ロビーには、モータの歴史とNIDECのかかわりの年表を展示しています。
その中で
とあります。Maxwellは19世紀最大の理論物理学者であり，Einsteinは20世紀最大の理論物理学者と言われています。そしてMaxwellの電磁場理論はEinsteinの相対性理論によって完成したといえます。
2006年に筆者は、佐野茂氏を共著者として『ピタゴラスの定理でわかる相対性理論』[1]を著わしました。
しかし、それはめざしている理論の前半にしか過ぎないものです。これとモータとの関係を書いて、モータの意味を深く考察する仕事が残りました。書こうとしても、うまい機会がなかったことと、果たしてわかりやすく書けるかどうかの逡巡がありました。難しくて分かりにくいのならまだしも、支離滅裂ではないかという心象を与えかねません。
しかし、その背景になることをメモしたいと思うのです。
電気力学の夜明け
アインシュタイン(Albert Einstein,1879 - 1955)は父親がミュンヘンで電気店を開いていたこともあって電気に深い関心をもち、叔父からも影響を受けていたと言われます。
当時19世紀末の電気技術といえば、照明・発電・電動が主なものでしたが、物理学・電気・通信工学の分野で大きな発見や発明がされた時代に重なります。一例を挙げると、
があります。
ただし、電動機と発電機の関係については1873年のウイーン万国博覧会で偶然に発見されていました。
マイケルソンの光速の観測結果は、古典的なニュートン力学の破綻を告げるものでした。そして真空を含めた空間を伝播する電磁波の研究とその応用の揺籃期でした。籠型誘導モータは、第１回に書いたように、導体が運動する磁界とともに運動しようとする作用を利用したモータであって、ブラシを使わないものでした。このことが重要です。
一方、数学はかなり進んでいました。学校ではユークリッド幾何学が重要科目でした。
アインシュタインもユークリッド幾何学の美しさに感嘆したことはよく知られています。非ユークリッド幾何学はできていましたが、学校の授業でそれについて生徒が知ることはほぼなかったのだと思います。
アインシュタインは1896年にスイスのETHに入学したのですが、一番勉強したかった電磁気学の先生がいませんでした。私どもにとってとても興味深いのは、物理実験の成績は最低でしたが、電気技術では高得点をえていたことです。
卒業後ベルンの特許局に勤務していた1905年、アインシュタインは5篇の論文をAnnalen der Physik（当時ドイツ語圏で最も権威のあった物理学論文ジャーナル）に発表しています。そのうちでノーベル賞を得たのが光量子仮説の論文で、3月論文とも呼ばれます。
特殊相対性理論は予想外の大魚
ここでは特殊相対性理論と知られる2つの論文のことを主題としようと思います。
アインシュタインの頭脳は異常であったと思います。父親の家業がモータの修理であり、彼は、モータの原理を説明し直そうという思いもあってZur Elektrodynamik bewegter Körper (運動物体の電気力学)というタイトルの論文を学位論文として母校に提出したものと想像してみます。これが有名な特殊相対性理論でした。この論文は、小魚をとろうとして、予想外の大魚が釣れたようなものです。
時間と距離についてはニュートン力学を破る理論ですが、マックスウェル（Maxwell）の電磁波の波動方程式と矛盾しない理論です。
マックスウェルの方程式には光の速度cが定数として入っています。当時すでに光は波動であることが分かっていたので、その波動を伝搬する媒体はいったい何かについて議論されエーテルという媒体が仮定されました。
では地球はエーテルに対してどんな速度で動いているのか、公転のために春と秋では違うはずだからその違いを観測しようとしたのだが、不思議な結果(エーテルは存在しなかった)になったのがマイケルソンの実験です。それを説明するためにアインシュタインはスイスのベルンで友人相手に議論をして考えていたのです。
この理論を理解できる先生がいなかったためか、学位論文としては引っ込めたようです。
世界で一番短い方程式!!
特殊相対性理論としられる6月論文がElektrodynamik bewegter Körperで、9月に、短編論文Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?を発表します。
この短編は
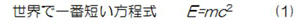
を導いたとされる論文ですが、彼はこの方程式としては記述していません。
このような意味を次の文章で記述したのです。
Gibt ein Körper die Energie E in Form von Strahlung ab, so verkleinert sich seine Masse um 
《訳》ある物体がエネルギーを光の放射の形で放出すると、その質量が
ちなみに、図１は、この論文を読みながら筆者が想像したものでアインシュタインの理論的モデルです。
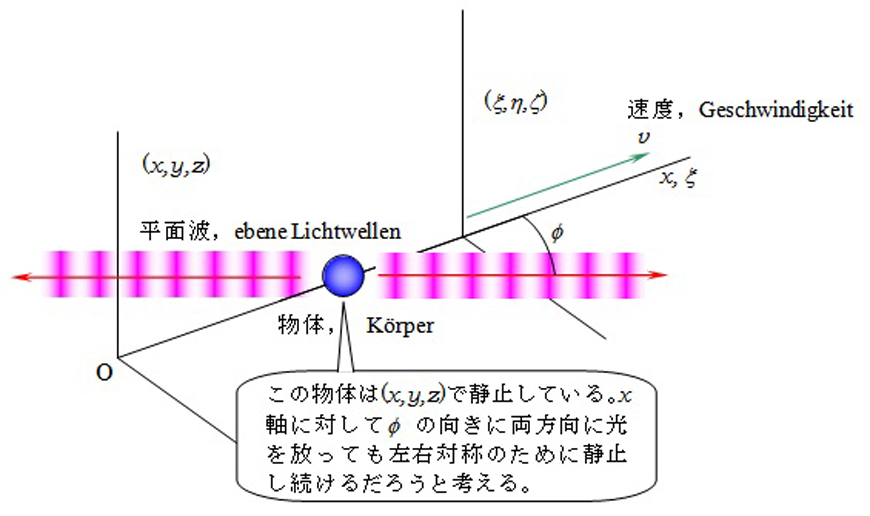
質量を電気現象で説明しよう
アインシュタインの
というのは彼の9月論文以前に、
アインシュタインはそれを引用しないで9月論文で類似のことを述べたとも解釈できるのですが、今ではアインシュタインにプライオリティがあるとされています。
ここを微妙に淡々と述べているのが、Chronik Osterreich（オーストリア歴史年表）の1904 年のページにある次の2行です。
Der Physiker Friedrich Hasenöhrl veröffentlicht seine “Theorie der Strahlung bewegter Körper” (1905 von Albert Einstein bestätigt).
《訳》物理学者フリードリッヒ・ハーゼンエールは運動物体の放射に関する理論を公表(1905年アインシュタインによって確証される。)
ハーゼンエール（Friedrich Hasenöhrl, 1874 - 1915）の論文は1904年のAnnalen der Physikに掲載された長編ですから、アインシュタインは当然みていたと思います。
ただし、これは黒体輻射の運動に関するもので、輻射エネルギーを質量換算するものだとして、(1)式に照らしあわせると係数が(3/8)になります。
Max Abraham（アブラハム）という若いドイツの物理学者が、ハーゼンエールの理論の積分計算にエラーにあることを指摘して、正しくは(3/8)であることをAnnalen der Physikに寄稿しています。
ここからが一つの論点です。それ以前に、英国のケンブリッジではラーモア (Joseph Larmor, 1857 – 1942)という偉い先生が、電子の質量の由来というか原因について考察して、それは電子の電荷に由来するという仮説を立てました。
そして質量mは電荷が形成する電磁エネルギーEに由来するものとして
ハーゼンエールもラーモアも光の速度に関しては古典論にしたがっています。そして、それぞれの理論がとても複雑です。それに比べるとアインシュタインの9月論文の理論は6月の相対性理論をもとにした考察から、手品のように少ない数学プロセスで導いています。
係数がアインシュタインの１なのかハーゼンエールやラーモアの3/4なのかは、難問だったのですが、やはり１であることが確証されたのは1960年代のようです。
このあたりを詳しく論じたのが大阪大学の(故)砂川重信教授です。どちらの係数が正しいかの議論よりも重要だったのが、上に記したように、この式の解釈です。
今日、
福島の原子力発電所の事故後の放射線汚染はそのことを如実に語っています。
ここでもう一つだけ加筆したいと思うのが, ニューヨークのAdelphi University (アデルフィ大学)のEugene Hechtの2009年の論文Einstein on mass and energy[5]のことです。彼もアインシュタインがE=mc2とは記述しなかったことを指摘して，これについてアインシュタインが1906年以降にどのように考察したのかを数多くの論文を引用して論じています。
非ユークリッド幾何と電気力学
特殊相対性理論は、時間を含めて4次元の双曲幾何によって説明できることにアインシュタインは気づいていませんでした。双曲幾何は非ユークリッド幾何の一つです。これは光や電波の速度が観測者の運動速度にかかわりなく一定値となるような理論です。
こう言い切ってしまってよいか迷うのですが、これを説明した世界で唯一の著作が筆者と佐野茂氏の『ピタゴラスの定理でわかる相対性理論』かもしれないのです。ただし、光の一定値が秒速30万キロメートルになることは説明できません。
その後、アインシュタインは重力と質量の関係を説明するために一般相対性理論というテンソル論を1915年に完成するのですが、このプロセスのなかでETH時代の旧友のグロスマンから(より広い非ユークリッド幾何である)リーマン幾何のことを聞いて共に学んでいます。コラムのアインシュタインの写真は、一般相対性理論を確立した絶頂期のころのものと思われます。
アインシュシュタインの理論に啓発されて、モータと発電機の電気力学－テンソル理論－を生み出したのがガブリエル・クロン（Gabriel Kron，1901 – 1968）です。
クロンはミシガン大学で学んでいますが、生まれはハンガリーでしたので、フォン・ノイマンと同じように、当時のギムナジウムではドイツ語で教育を受けていたと思われます。ですから彼はアインシュタインの論文を原語でも読んだに違いないと思います。
ただし、彼の理論の表題はNon-Riemannian Dynamics of Rotating Electrical Machineryであり、リーマン幾何的ではありません。空間的には2次元(互いに直角の関係にある2相)のユークリッド的な空間で展開した理論です。なお、クロンの電気力学はほとんどのモータを包含するのですが、扱えないのが前回のテーマであったヒステリシスモータとSRモータ、そして超音波モータです。また空間的に3次元の扱いが必要になる最近のモータには若干の工夫が必要かもしれません。
クロンもシュタインメッツと同じようにGeneral Electric 社でモータの理論に貢献しました。次回は英国の物理学者ポインティング（J.Poynting）の理論を引用して、モータ構造にある空隙の不思議について論じてみようと思います。ここですべての種類の電磁気モータの統合理論を語ることになります。
(Albert Einstein 1879-1955)
アインシュタインはドイツ生まれだったが、型にはまった教育になじまず、スイスのチューリッヒ・ポリテクニークの物理と数学の教師養成コースを受験した。そのとき正規の入学許可年齢より2歳も若かったのに物理と数学の成績がよかった。しかしフランス語などの点数が低かったのでアーラウのギムナジウムでの準備をしてから入学が許可されることになる。
当時の、物理学の話題の中心は光の伝播速度のことだった。すでにマイケルソン・モーリーの計測によって、光は音波などとは違って伝播速度が観測者の位置や速度に関係なく300,000km/secであることが分かっていた。つまり宇宙の絶対的基準としてのエーテルが否定されていたが、16歳の少年アルバートもしきりにこの問題を考えていた。アーラウで寝起きをともにした友人にイタリア人のベッソーがいた。
ポリテクニークを卒業したが、念願の教職になかなか就けずにクラスメートだったグロスマンの助けによってベルンにある特許局に勤務しながら物理の根本的な問題について考えては論文を書いた。アインシュタインの優れた点の一つは友人の活用だった。物理の考察のために物理を学ぼうとする友人をみつけて彼に個人レッスンをしながら考察した。特許局にベッソーを就職させたのだが、光について議論の相手がほしかったのだ。光が波動であることがわかっていたのだが、1905年の3月論文でアインシュタインは光には粒子のように最小単位があることを提唱した。これが後にノーベル賞論文になった。光速一定を理論づける論文を同年6月に発表した。これは当時の論客として知られるオランダのローレンツやフランスのポアンカレを超えるもので特殊相対性理論と呼ばれる。
友人グロスマンの助けによってリーマン幾何学を勉強して、重力に関する一般相対性理論を発表し始めたのは1911年からである。そして1919年、英国のアーサー・エディントンによる日食観測によって、光が太陽の重力によって曲がることが証明されてアインシュタインは一躍有名になった。
- [1] 見城・佐野『ピタゴラスの定理でわかる相対性理論』，技術評論社
- A. Einstein: Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig, Annalen der Physik, 1905. pp.639-641
- [2] ピタゴラスの定理でわかる相対性理論補講：第10回
http://gihyo.jp/science/serial/01/pythagoras/0010 - 砂川重信：理論電磁気学，紀伊国屋書店, 1999
- Eugene Hecht: Einstein on mass and energy, American Journal of Physics, Vol.77, No.9, September 2009, pp.799-806
