Quest For Motors' Hidden Abilities and New Potentials
Lecture 12: Special theory of relativity derived from Siemens’ unipolar machine
Continuing from the last article, I would like to consider non-Lorentz forces and the theory of relativity. Electrodynamics and relativity theory are closely related. Einstein was the first to realize this fundamental relation. But Maxwell had begun arguing that light is an electromagnetic wave around 1864, which prepared the path for Einstein’s breakthrough. In 1905, Einstein presented five epoch-making papers, two of which were on his ideas about special relativity. In the first paper On the Electrodynamics of Moving Bodies, the word “Unipolarmaschinen” appears only once in parenthesis, as seen in Figure 1. This is the main theme of this article, and has also been my long-standing question.
This question was resolved by an article titled “Einstein in München” [1], which gave a short history of Jacob Einstein and Co., a venture manufacturer of ark lamps and dynamos (=generators) in Munich. The company’s workshop was the environment in which Albert Einstein spent his childhood and began to learn about electricity and magnetism. Stefan Siemer, the article’s author, says
It is scarcely known that Einstein, as a theoretical physicist, repeatedly dealt intensively
with technical apparatus and inventions.
According to him, Einstein wrote in 1930 in a letter, “I never stopped working on technical things. This was also beneficial for scientific research.”
The article further says:
… a dynamo machine designed by Werner Siemens in 1881 – known as a unipolar machine – was the cause for him to think deeply about the principle of electromagnetism in a new way and mention it in his paper on the special theory of relativity.
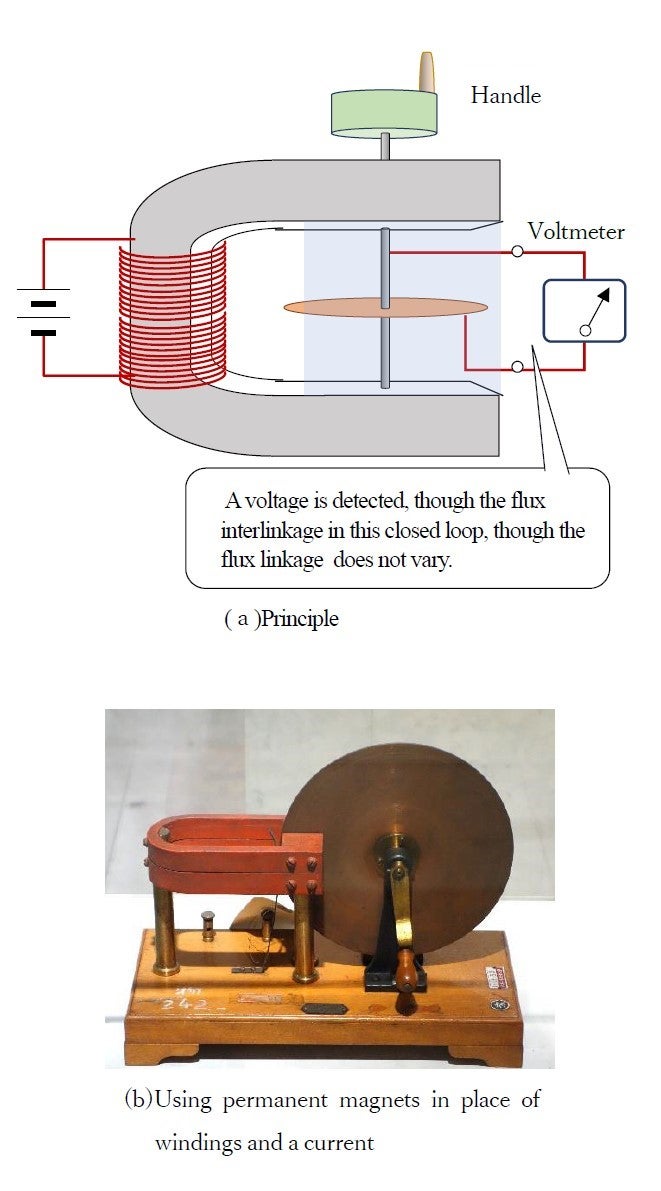
The photo in Figure 2 is a unipolar machine I set up to examine Einstein’s idea, and Figure 3 illustrates the setup to measure the generation of voltage.
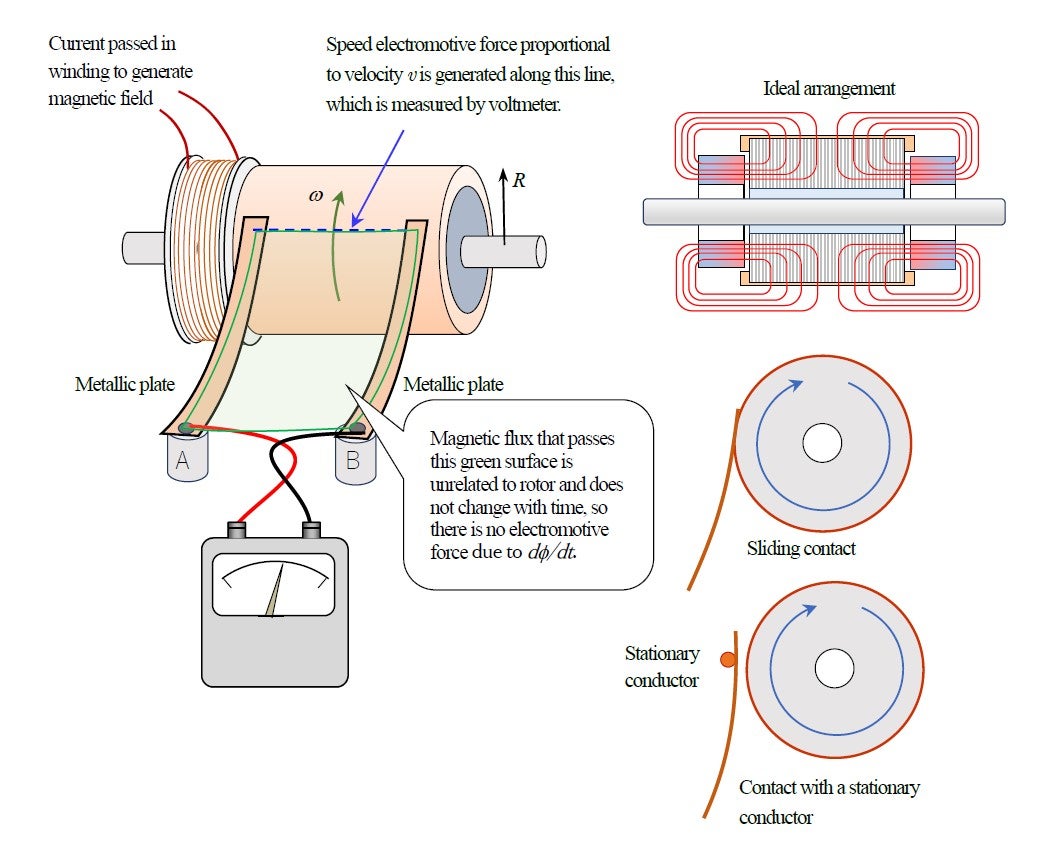
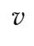. If the two metal plates are connected by a stationary conductor, no voltage is measured.Electromagnetic motor and Galilean transformation - Reexamination of fundamental physical laws
Those who have attended a course on or taught themselves relativity may be quick to conclude that the theory of relativity deals with the Lorentz transformation, but the Galilean transformation is the starting point. Here, we will review some basic facts about the motion of objects and electromagnetic forces, as shown in Figure 4. Fleming explained the complex relationship in an easy-to-understand manner; Figure 4(a). Fleming explained the complex relationship in an easy-to-understand manner;
Relative motion
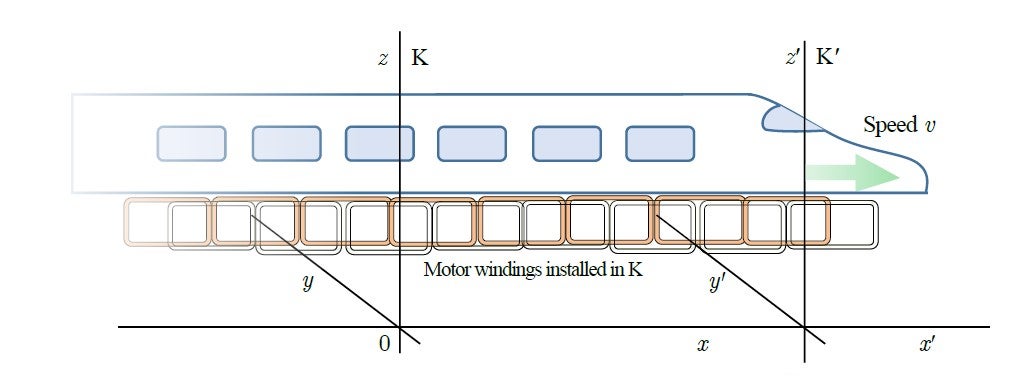
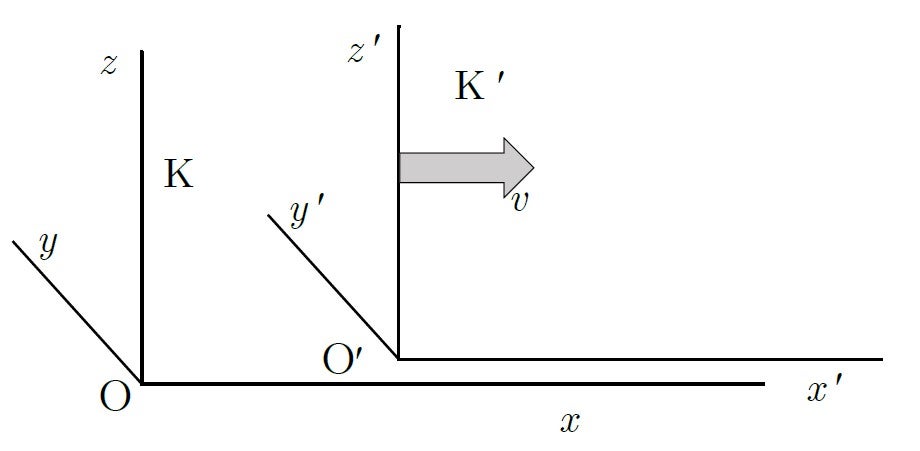
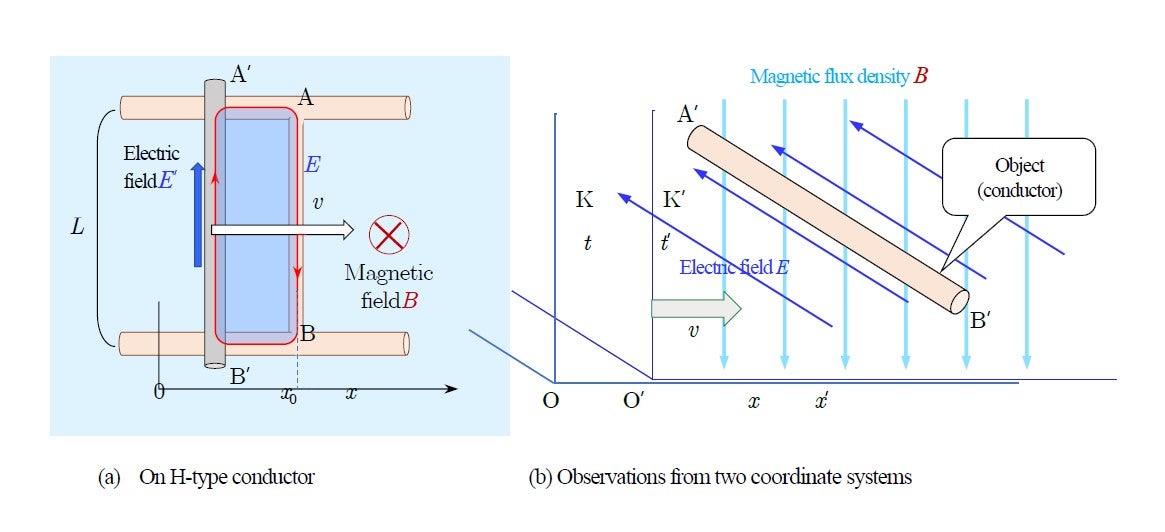
The relationship between the stator and rotor is one of relative motion. Let us consider a linear motor, as shown in Figure 5, instead of a rotary motor. In this figure two coordinate systems K and K’ are set: the K coordinate frame is fixed on the stationary windings, while K’ is fixed with the linear train which is moving in the 
-direction with speed 
. Their relative movement is depicted in Figure 6. In connection to this figure I’m going to put forth a question about a certain asymmetry that was whispered among the engineers at the factory run by Albert’s uncle Jakob Einstein when Albert was a little boy. You will see that what seems obvious is not so obvious.
Between the two systems in Figure 6 there is the following relationship:
Now, let's take a closer look at Fleming's right-hand rule on Figure 4(c) . When the magnetic field 
is cut by a moving conductor, an electric field 
is generated, where Figure (a) the fingers of the right hand show the directions of each vector. This phenomenon is expressed by:
where 
= Electric-field strength in stationary system
，
= Electric-field strength in system
Formula (2) has the same form as (1). Most readers may casually read this and say, "Oh, I see.", but some readers may think, "What is this! This expresses a commonality between space-time (, ) and electromagnetic fields ( , )! Is it true?"
Next, let's consider a symmetry related to relative motion. in Figure 6 is a moving system, but for the observer who is moving with it, this is a stationary system, and is a coordinate system that moves with 
. If we rearrange the left and right terms in the two equations above, we get the following equations.
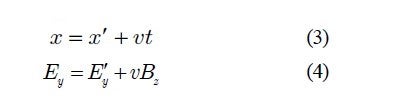
Great! The symmetrical relationship of relative motion appears to hold for electromagnetic systems as well. However, this was true up until Faraday. With the advent of Maxwell, an asymmetry arose. Einstein solved this problem and proposed a new symmetry, which is the special theory of relativity.
moving at in the -direction in stationary frame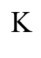 
Before we discuss this, we shall take a closer look at an important observation made by Faraday. Figure 7 shows his experiment with a generator, which he allegedly conducted in 1831. In this experiment a current was detected when a resistor was placed across the two terminals. Today it is called a unipolar generator, but I don't think that term existed at that time. Also, we may imagine that it was an experiment in relation to Arago's disk. If we look only at the closed circuit shown here, the magnetic flux linkage is constant whether the disk rotates or not, so the law of electromagnetic induction
cannot by itself explain the generation of electromotive force.
When there is motion in the elements that make up the closed circuit, an electromotive force is generated by cutting of the magnetic field. In Faraday's unipolar machine, however, it is not simple to theoretically treat it using mathematical equations because the velocity of the conductor in question varies with the distance from the axis. Meanwhile, the engineers in Jacob Einstein's factory were discussing Siemens’ unipolar generator, and “Unipolarmaschine” must have been used as a technical term. Its construction was similar to the one shown in Figure 3, and the motion velocity is 
everywhere. Now, I would like to make a few additions using Figure 8 and Figure 8.
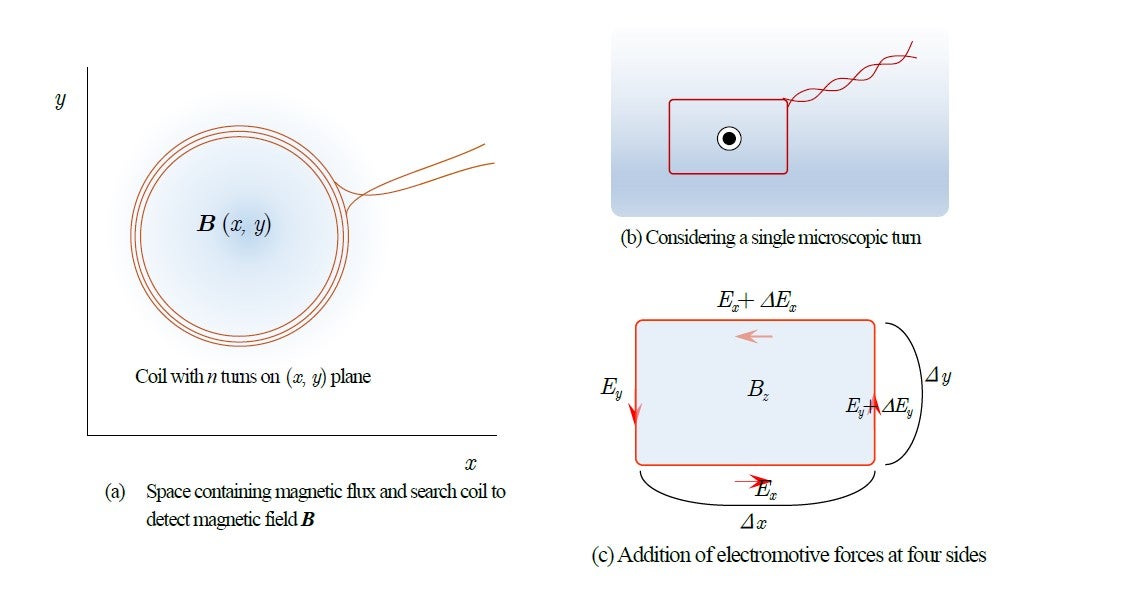
Figure 8 shows how to derive one of Maxwell's equations:
Here, principle of electromagnetic induction, equation (5), is applied to a tiny rectangular coil with a single turn, where the relationship between the electric field along the coil and the magnetic flux surrounding the coil is as follows:
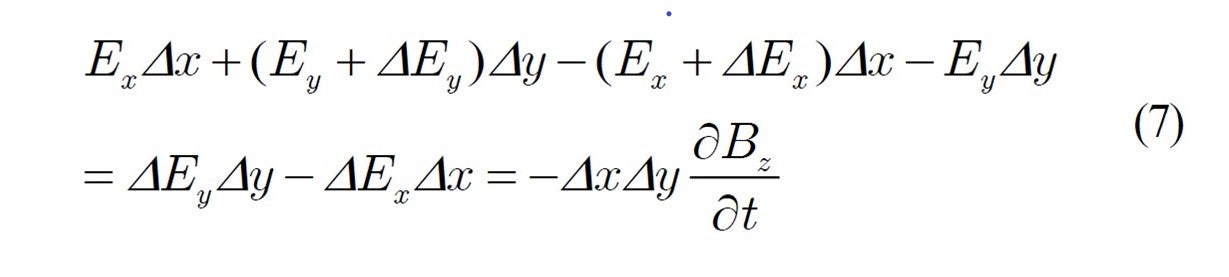
From this, we obtain
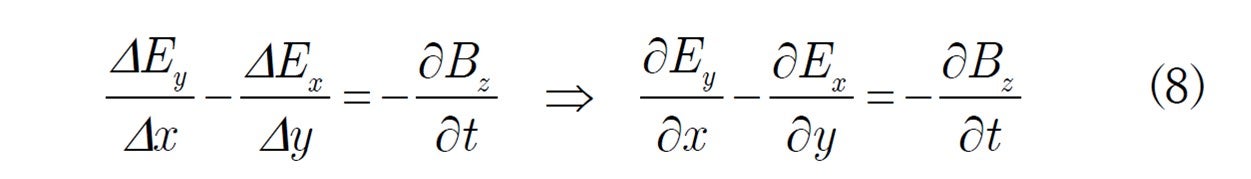
By generalization we obtain above (6). This was the case with a coil at rest.
Next, let’s apply (5) to the case of the H-type conductor in Figure 9, where the sliding conductor A’B’ is in motion. Here, both the magnetic field and the electric field are uniform. Since the area surrounded by the red integral path changes with time, the magnetic flux linkage also changes with time. And (2) is obtained, which is regarded as Fleming's right-hand rule.
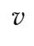to derive the right hand rule 
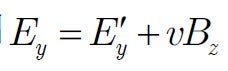.Asymmetry appears
Asymmetry appears 
can be modified to 
.
Readers may know that it was James Maxwell, born in Scotland, who took Faraday's discoveries and insights seriously. He assumed that a change in the electric field can generate a magnetic field, similar to how changes in the magnetic field generate an electric field. Based on this assumption, in 1864 he rewrote Ampere’s integral formula, using differential expression, as follows:
where 
is electric-field flux density vector.
(Note, however, that the vector analysis notations as we know them today was later developed by Heaviside.) Here, 
is the actual current density. Actual current is the current produced by electrons moving in a vacuum or in a conductor. Meanwhile, the second term 
on the right-hand side is called the displacement current. To examine the essence of the matter, we consider the case where 
:
Since this has a similar form to equation (6), the following algebraic form is obtained from association:
By putting 
, equation (4) can be rewritten as
Since (11) and (12) hold simultaneously, we obtain:
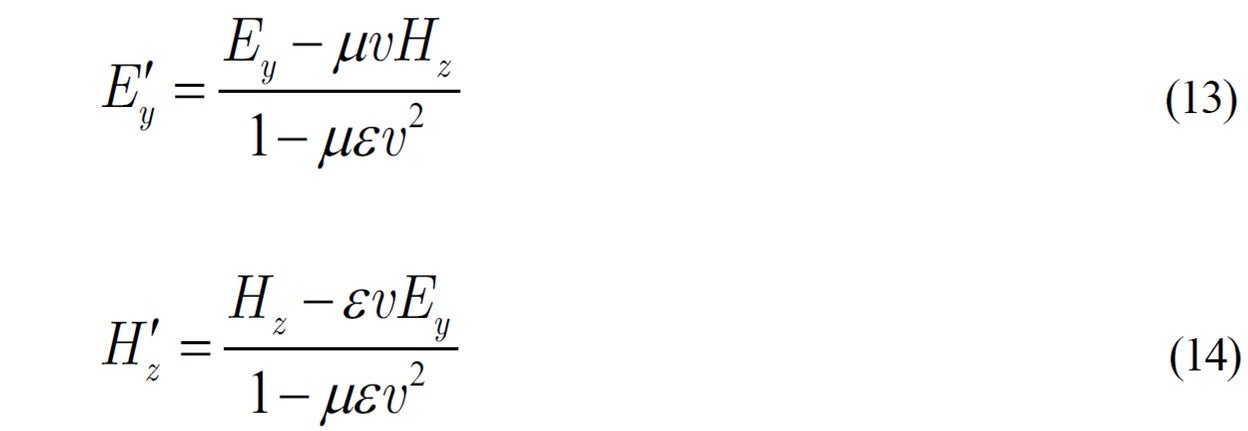
Thus the symmetry like that in (3) and (4) has been lost and an asymmetry comes out). In other words, a contradiction appears in plain expected relativity. As a practical matter, 
, so 
is negligible compared to 1, and symmetry holds as an approximation. But theoretically, it doesn't make sense.
Elimination of asymmetry – resulting in Lorentz transformation of the electromagnetic field!
Einstein says in his 1905 paper that he resolved this question. Instead of the rambling explanation of this paper, let's use a simple linear algebraic approach here to solve this essential matter. In place of (13) and (14), using coefficient 
, we put
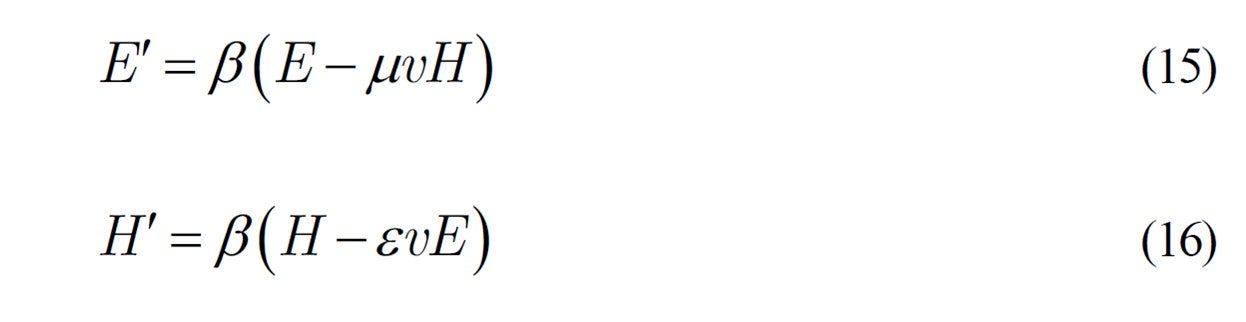
Here the subscripts are omitted for simplicity.
Let's rewrite this using a matrix with a first-order transformation expression:
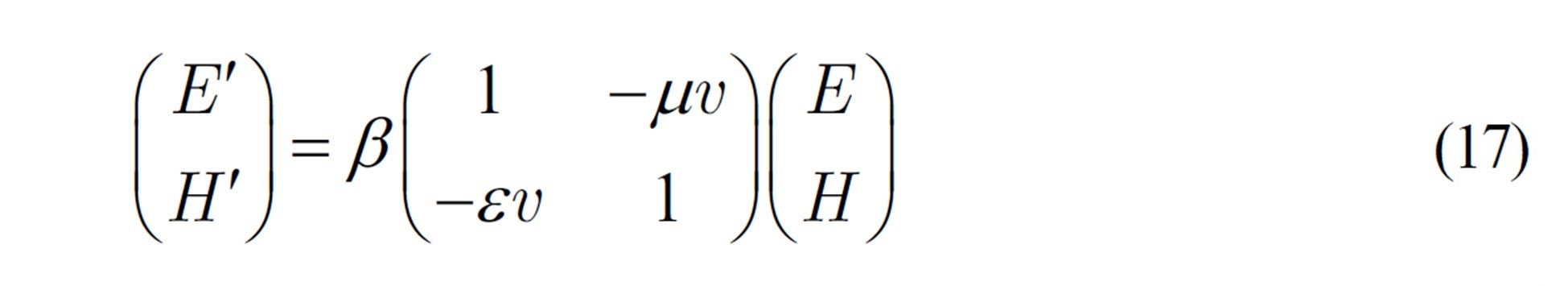
where the determinant of the transformation matrix is
Using this, the above equation (17) can be written:
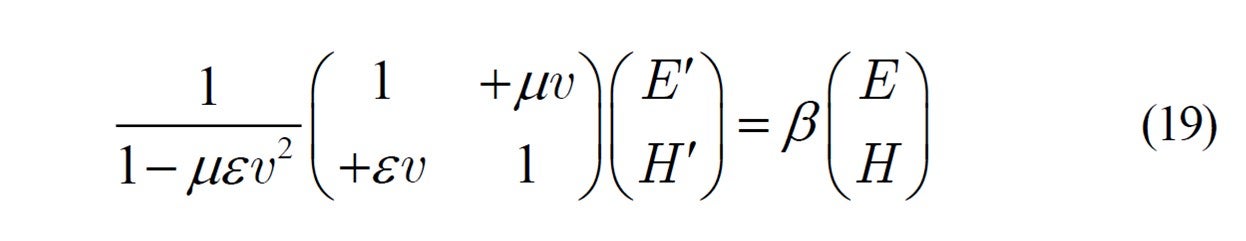
from which we get
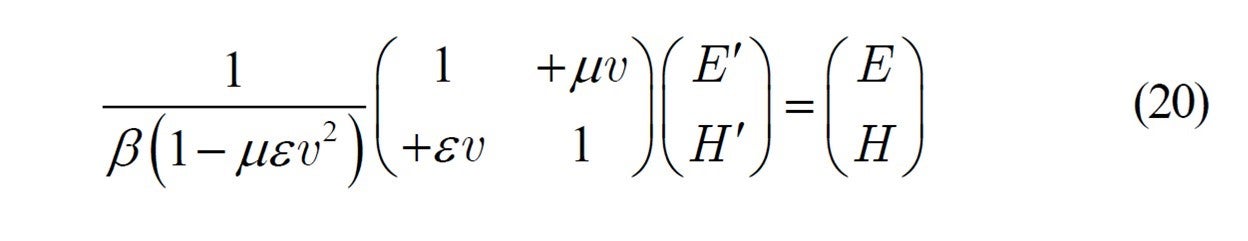
By replacing with in (17), symmetrical relationship must appear:
From comparison with (20), must be:
What does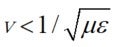
mean?
In order for in equation (22) obtained above to be a real number, 
is required. What exactly does this mean? The rotor we are currently considering in the unipolar machine is composed of a metal such as copper or aluminum, and its magnetic permeability 
and permittivity 
are almost the same as in a vacuum. Then, 
is the speed of light 
.
We thus have
which is the key factor that Lorenz presented!
Lorentz transformation of spacetime
Now, will Maxwell's electromagnetic field equation itself be changed to include ? No, it is not necessary when the following spacetime relationship described in terms of the Lorentz transformation is taken into account.
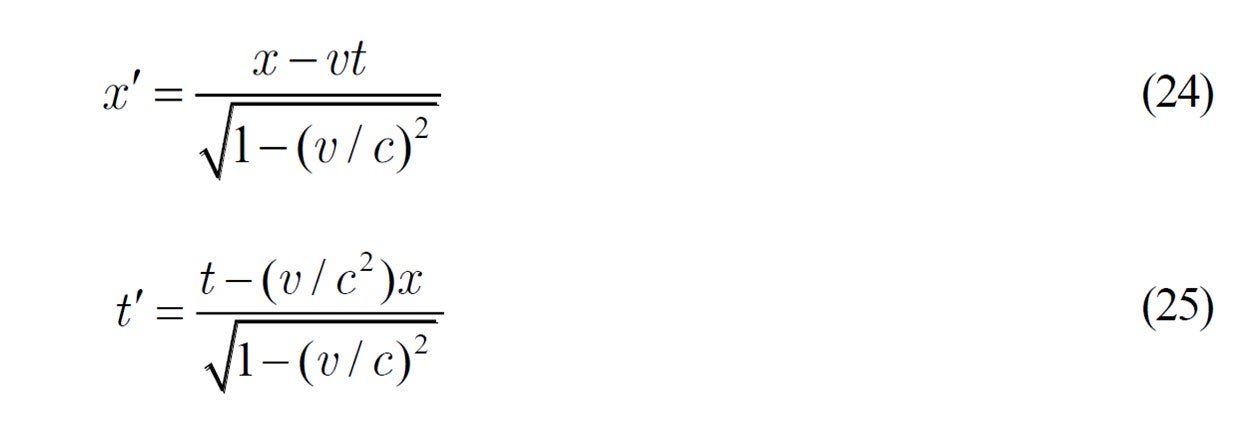
Note that if 
the position and time of the moving system become imaginary numbers. And if 
they become 
, which is unrealistic. Therefore, the velocity of relative motion must satisfy
In other words, even if we design a high-speed spacecraft, it will be unable to exceed the speed of light .
Principle of constant speed of light
The speed of light is The speed of light is 
and permittivity 
. Assuming that we cannot distinguish between a stationary vacuum and a moving vacuum, the speed of light is independent of the speed of the light source. 
is the speed limit and cannot be exceeded. “Let's use this as an axiom to unify electromagnetic theory and mechanics.” I think this was the young Einstein's idea of electrodynamics. Will readers easily accept Einstein's theory? I think it's natural to not be easily convinced. Andrew Warwick's Masters of Theory [2] describes the difficulty that scholars at Cambridge University, which has a long tradition in theoretical physics, experienced before they finally accepted the theory of relativity around 1919.
References
１．Stefan Siemer : Einstein in München, Kultur & Technik, 02/2005
２．Andrew Warwick：Masters of Theory, University of Chicago Press, 2003
