Quest For Motors' Hidden Abilities and New Potentials
Lecture 3: Einstein's Theory of Relativity and its Relation to Motors
I have so far covered two legendary figures in the world of motor - Nikola Tesla and Charles P. Steinmetz, and posted a photo of Albert Einstein visiting Steinmetz. This third article covers Einstein and mysteries about motors.
The showroom on the first floor of the Nidec Research and Development Center exhibits a chronological table that shows how Nidec is related to the history of the motor.
The chronical table shows:
In 2006, I co-authored with Mr. Shigeru Sano a book, “Pitagorasu no Teiri de Wakaru Sotaiseiriron (The Theory of Relativity Can Be Understood with the Pythagorean Theorem).”[1]
Publishing this book, though, takes me only to the halfway point of the way to reach the theory I am attempting to reach: There is still work of writing on how the theory is related to the motor in order to have an in-depth analysis on it. There were not good opportunities for me to write the relations even though I tried to so, while it was unclear to me as to whether I would be able to write the way readers can understand the relations. What I write, I thought, may give readers an impression that it is incoherent, rather than that it is difficult to understand. But, here is some background information that led me to explore this problem
Dawn of Electrodynamics
Einstein (1879 - 1955), whose father ran an electrical store in Munich, Germany, is believed to have had a deep interest in electricity, and been influenced by his uncle as well.
The mainstream of the electrical technology at the end of the 19th century, when Einstein was alive, were illumination, power generation, and electroactuation, but it was also the time of major discoveries and inventions in the areas of physics, electricity, and communication engineering. Here are some examples:
The relations between the electrical motor and the electrical generator, though, were found by coincidence in the 1873 Vienna International Exhibition.
With the result of the observation of the speed of light by Michelson came the collapse of the classical Newtonian dynamics, while it was also a seminal period of the research and application of electromagnetic waves, which travel various forms of space, including vacuum. The squirrel-cage induction motor, as I wrote in the first article, is a motor that utilizes a mechanism where a conductor tries to move together with a moving magnetic field, and, importantly, the motor does not require a brush.
During this time, mathematics was well advanced, and the Euclidean geometry was a critical subject at school. It is a well-known fact that Einstein was deeply moved by how beautiful the geometry is. I believe that, though the non-Euclidean geometry had been established, students hardly had a chance to know about it.
Einstein entered ETH, a Swiss college, in 1896, but only to find that there were no teachers of electromagnetism, which he wanted to learn most. Interestingly, though, Einstein’s physics experiment score was the poorest of all the students in his class, he scored well in electrical technology.
In 1905, while working at a patent office in Bern, Switzerland, after graduation, Einstein published five theses in Annalen der Physik, the most prestigious physics paper journal in the then German-speaking sphere. One of them, the paper on photon hypothesis that won him a Nobel prize, is also known as the March paper.
Unexpected Success of the Special Theory of Relativity
This section focuses on two papers known as covering the Special Theory of Relativity.
Einstein’s brain must have been abnormal. With his father in a motor repairing business, Einstein, probably wanting to convince him with the principles of the motor, must have submitted an academic dissertation titled Zur Elektrodynamik bewegter Körper (Electrodynamics of Moving Bodies) to his old school. This dissertation, as it turned out, was about the famous Special Theory of Relativity. It is as if you had unexpectedly caught a large fish while trying to catch a small one. This Theory, which defies the Newtonian dynamics in terms of time and distance, does not contradict Maxwell’s wave equation of electromagnetic waves.
Maxwell’s wave equation contains “c” as the speed of light. Back then, light had already been known to be composed of waves, and, after a series of discussion on what propagates the waves, a medium called ether was hypothesized to exist. It was in Michelson’s experiment that produced a mysterious result (which proved that ether does not exist) after attempts to observe the speed of Earth against ether as well as the difference in the speed, which should fluctuate between spring and autumn as Earth revolves. To explain the result of this experiment, Einstein discussed and contemplated the result with his friends in Bern, Switzerland. In the end, Einstein seems to have withdrawn this academic dissertation, probably because no teachers could understand what it is about.
The World’s Shortest Equation Ever!!
Following the paper on the Special Theory of Relativity, Elektrodynamik bewegter Körper, known as the June Paper, Einstein published a short paper called Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? (Does the inertia of a body depend on energy content) in September.
Though this paper is believed to contain the world’s shortest equation,
Einstein did not write this equation itself. Instead, he expressed what it means in the following paragraph [2]:
Gibt ein Körper die Energie E in Form von Strahlung ab, so verkleinert sich seine Masse um 
Translation: “If an object releases energy E in the form of radiation, then its mass decreases by 
It is not excluded that with objects whose energy-content is variable to a high degree (e.g. with radium salts) the theory may be successfully verified.
If the theory corresponds to the facts, radiation transfers inertial mass between the emitting and absorbing objects.”
Illustration I shows Einstein’s theoretical model that I created in my imagination while reading this paper.
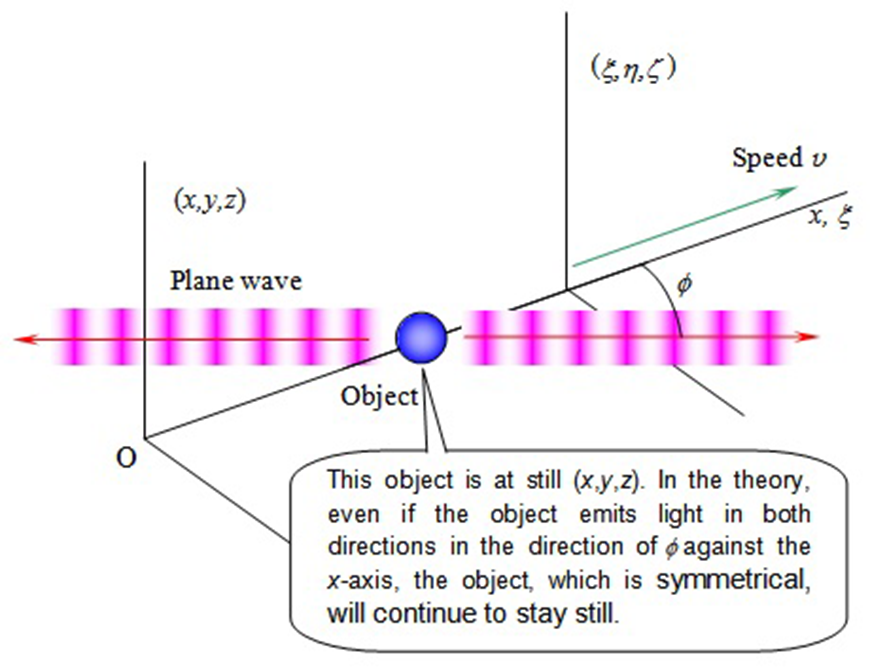
Explaining Mass with Electrical Phenomena
Many stories exist about Einstein’s 
This is because that a theoretical equation 
Einstein may have made a similar statement in his Paper without quoting the above equation, but the priority is believed to on Einstein now.
Two lines on the page for year 1904 of Chronik Österreich (Chronicle of Austria) states this fact in a detached tone:
Der Physiker Friedrich Hasenöhrl veröffentlicht seine “Theorie der Strahlung bewegter Körper” (1905 von Albert Einstein bestätigt).
Translation: “Physicist Friedrich Hasenöhrl publishes the Theory of Radiation of Moving Bodies (verified by Albert Einstein in 1905).”
Einstein certainly must have seen this full-length theory by Hasenöhrl (1874 – 1915), which was published in the Annalen der Physik journal in 1904. However, if you assume this theory is regarding movements of black-body radiation that converts radiant energy into mass, and if you compare it with Formula (1) above, the coefficient will be 3/8. The then young physicist named Max Abraham of Germany wrote to Annalen der Physik, pointing out an error in the integral calculation in Hasenöhrl’s theory, and stating that the proper coefficient is 3/8.
Here is a point of argument: Prior to the publishing of the above theory, a well-known professor named Joseph Larmor (1857 – 1942) of Cambridge, the U.K., after discussing the origin/cause of electrons, formed a hypothesis that electrons are originated in their charge, and assuming that mass (m) is originated in the electromagnetic energy (E) formed by the charge, derived the
In the area of the speed of light, both Hasenöhrl and Larmor followed classical theories, each of which is truly complex. Einstein, on the other hand, based on discussions on the Theory of relativity in his June Paper, derived the theory in his September Paper, using magically fewer mathematical processes.
It was highly difficult to determine whether the proper coefficient is 1 as predicted by Einstein or 3/4 as stated by Hasenöhrl and Larmor until 1960’s, when, as I understand, 1 was proved to be the proper coefficient. Late Professor Shigenobu Sunagawa of the Osaka University explained the process of proving the coefficient in detail. How to interpret the above equation was more important than the discussion on which one of the coefficients is correct.
Today,
Non-Euclidean Geometry and Electrodynamics
Einstein did not realize that the Special Theory of Relativity can be explained by four dimensional hyperbolic geometry, including time. Hyperbolic geometry, part of the non-Euclidean geometry, is a theory where the speed of light or radio waves becomes constant regardless of the observer’s movement velocity. It makes me hesitate to state this, but my and Mr. Sano’s literary work, “Pitagorasu no Teiri de Wakaru Sotaiseiriron (The Theory of Relativity Can Be Understood with the Pythagorean Theorem)” is probably the only literary work in the world that explains this fact, except for the part that the constant value of light becomes 300,00 km per second.
Then, Einstein completed his work on the General Theory of Relativity, a tensor theory to explain the relations between gravity and mass, in 1915. It is during this process of establishing the Theory that Einstein heard of the Riemann geometry (a category of non-Euclidean geometry that covers a wider area) from, and studied it together with, Grossmann, with whom he learned at ETH in Switzerland. The photo of Einstein in the column below is believed to have been taken around during the prime of his life, when he established the General Theory of Relativity.
Inspired by Einstein’s theory, Gabriel Kron (1901 – 1968) created a tensor theory of the electrodynamics of motors and power generators. Kron, Hungary-native who studied at the University of Michigan, is believed to have been educated in German at gymnasium, as John von Neumann did. He therefore must have read Einstein’s theories in their original language.
Kron’s theory was, though, titled “Non-Riemannian Dynamics of Rotating Electrical Machinery,” not Riemann-geometric. This theory was developed based on a two-dimensional Euclidean space (consisting of two phases perpendicular to each other). Kron’s electrodynamics covers almost all motors, except for the hysteresis, SR, and ultrasonic motors discussed in the previous article. In addition, some measures may be necessary for recent motors, which require a three-dimensional space.
Like Steinmetz, Kron contributed in the area of motor theory at General Electric Company. In the next article, I will try to discuss the mystery about gaps in motor structures based on the U.K. physicist John Henry Poynting’s theory. With that article, I will discuss the integrated theory of all kinds of electromagnetic motors.
(1879-1955)
Though born in Germany, Einstein did not fit in the country’s stereotyped education system, and took the entrance examination for the physics and mathematic teacher training course of the Swiss Federal Polytechnic School in Zurich, Switzerland. He was two years below the official age to be admitted to the school, but excelled in physics and mathematics. However, due to poor scores in French and other subjects, Einstein was admitted to the school after making preparations at gymnasium in Aarau.
The focus of physics at that time was the propagation velocity of light. The Michelson-Morley experiment has already revealed that the propagation velocity of light is, unlike that of sonic waves, etc., 300,000km/sec regardless of the location or speed of the observer. In other words, the existence of ether, an absolute cosmic standard, was denied as a notion. Nevertheless, Einstein, age 16 at that time, was among those who were constantly thinking about this issue. One of the people with whom Einstein lived in Aarau is an Italian named Michele Angelo Besso.
Unable to find his ideal job of teaching after graduating from the Polytechnic School, Einstein, with assistance of Grossmann, his classmate, worked at Bern’s patent office, where he contemplated and wrote papers on fundamental physics problems. One of the areas where Einstein was excellent was the utilization of his friends: He would find friends wanting to learn physics, and give them private lessons to contemplate physics. The reason he had Besso employed at a patent office was to have someone to discuss light. Though it had already been understood that light is comprised of waves, Einstein propounded in his March 1905 Paper that light, like particles, has a minimum unit, and later won a Nobel prize for that. Einstein then published a thesis that the speed of light is constant in June the same year. This thesis, which exceeded the theories of the debaters at that time, Hendrik Antoon Lorentz of the Netherlands and Poincare of France, is called the Special Theory of Relativity.
It is from 1911 that Einstain, with assistance of his friend Grossmann, studied the Riemann geometry, and started publishing papers on the General Theory of Relativity related to gravity. Einstein was catapulted into fame in 1919, when the eclipse observation by Arthur Stanley Eddington of the U.K. proved that light is bent by solar gravity.
- [1] “Pitagorasu no Teiri de Wakaru Sotaiseiriron (The Theory of Relativity Can Be Understood with the Pythagorean Theorem)” by Takashi Kenjo and Shigeru Sano, Gijutsu-Hyohron Co., Ltd.
- [2] “Pitagorasu no Teiri de Wakaru Sotaiseiriron: Dai 10 Kai (The 10th Makeup Class on ‘the Theory of Relativity Can Be Understood with the Pythagorean Theorem’)”
http://gihyo.jp/science/serial/01/pythagoras/0010 (in Japanese)
