2-1-5 有铁芯槽的直流马达的旋转原理

现在让我们回到最初的疑问。与空气相比，铁具有可轻易通过约1000倍磁气的性质。由于具有这种性质，有铁芯槽的转子如图2.18 所示，磁力线会集中到铁芯，线圈部的磁场会非常弱。这样的话，“在磁场中放置的电线上”的BLI定则及“电线会横穿磁场”的反电动势常数换算的前提条件就不成立。

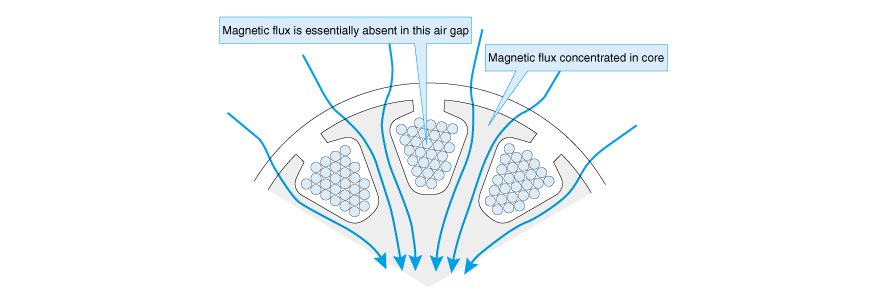
此外，线圈不通电时，用手转动马达轴的话，在转子的齿和永久磁铁的作用下，也会感到有一定的阻力。这称为齿滞。

仅仅利用BLI定则和反电动势常数换算来介绍，无法讨论齿滞的影响。

下面针对有铁芯马达的扭矩发生原理从2个侧面尝试说明。

（A）通过磁力线的张力进行介绍

磁铁之间相互吸引或排斥的力或磁铁吸引铁钉的力无法使用BLI定则做出说明。即，基于磁作用的力，作为基于磁场中电流的作用，很难做出说明。实际上，在物理学深层次上是有关系的。

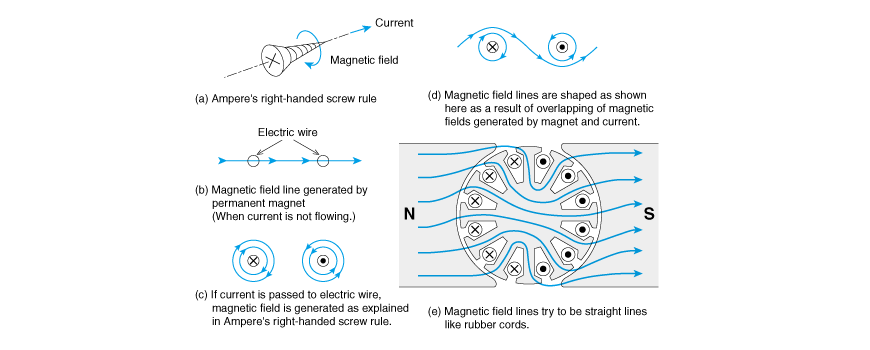
这可以利用磁力线的概念进行综合说明。磁力线具有橡皮绳那样紧缩的作用。将电线靠近铁的附近，然后通电，将磁力线进行弯曲，则会产生一种想让其拉直的力。图2.19 就是利用该原理介绍直流马达的扭矩如何发生。

＜小知识＞和（点和十字）

图2.19 中的称为点，表示从纸的背面进向纸正面的方向。

相反，称为十字，表示从自己这边朝向纸正面的方向。通过图2.19（a）与螺旋的图对应起来会比较容易记住。

在马达的发电作用项目中，我们已经介绍了扭矩常数与反电动势常数基本上是相同的。现在重新观察图2.8 会发现，即使是有铁芯槽的模型用马达，也会发生反电动势。

这与其是说电线横切磁场，不如理解为像图2.20 所示那样，作为与线圈交链的磁通的时间性变化的比例，发生反电动势，其通过电刷和整流子进行整流（AC→DC转换），表现为直流的反电动势常数换算。

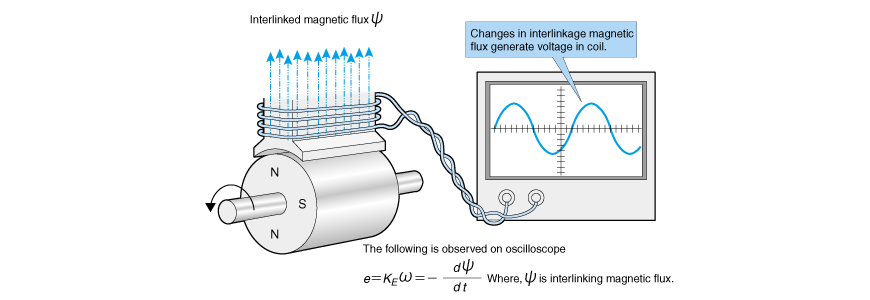
像（2.9）公式中所看到的那样，K_E和K_T是一样的。因此，不对扭矩进行解析，而观察反电动势常数换算，将计算得到的K_E直接作为K_T，就能够计算扭矩。这是第二种说明方法。

那么通过这种方法该如何理解齿滞呢？简单来说，只要加上该成分即可。

齿槽力矩的计算方法有几个，但都非常复杂。

本书将不做详细介绍，只介绍这种方法也可以计算有铁芯马达的扭矩。对此的详细记载，请阅读参考资料[1]。

［文献］

［ 1 ］见城・永守：新・无刷马达，第5章，综合电子出版社

本书中展开的理论除基本内容外，还介绍了至今仍有专家并不了解的基本原理，是世界上唯一的一本书。对于初学者来说可能有点深奥，如果想成为马达方面的专家，请务必仔细阅读该书。

＜小知识＞交链

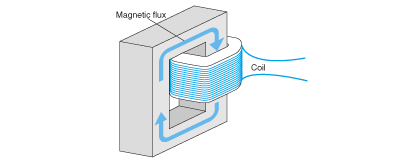
磁通与线圈，如下图所示，像锁链那样进行连接。

这就是交链一词的意思。在马达和变压器中，与电线卷数相关可使用该术语。所谓交链磁通，是磁通（单位：Wb韦伯）与线圈圈数之积。