2-1-3 直流马达的转速和反电动势常数换算
为了进一步了解扭矩常数KT,我们再想一下马达旋转时的情况。
这与马达的发电作用相关。
发电作用与右手法则
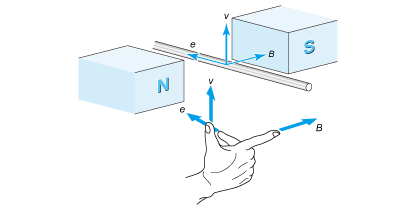
e = BLv ……(2.5)
e:发生电压、反电动势常数换算[V]B:
磁束密度[T]
L:磁场中的电线长度[m]v:速度[m/s]
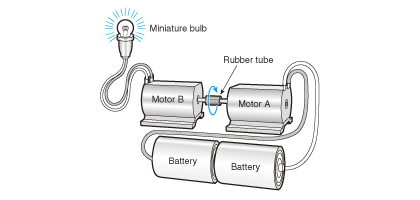
如图2.6 所示,将2个马达连接起来,在其中一个马达上连接小电灯泡,另一个马达上连接电源,旋转马达,则小电灯泡会亮。
从这个实验可以知道直流马达具备发电作用。
这一次,图2.7 所示,不通电流,将电线以速度v移动,使其横穿磁场,则电线中会出现电压e 。将其与之前的图2.2 进行对比。
该电压的方向由弗莱明右手法则决定。该方向与图2.2 中的电流方向相反,会起到减小电流的作用,因此,称为反电动势常数换算。电线作为马达线圈的一部分,参考图2.3 ,电线速度v可表述成v=ωR。因此,该电线上出现的反电动势常数换算变成以下公式。
e=BLRω ……(2.6)
ω:转速[rad/s] R:旋转半径[m]
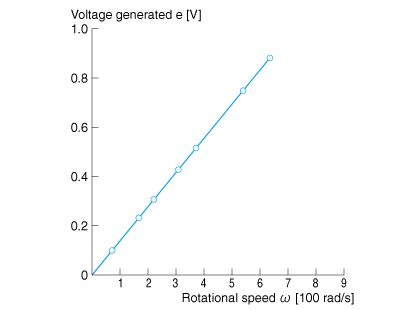
即,反电动势常数换算与转速ω成正比。
在实际的直流马达中,作用在所有线圈上的反电动势常数换算会加起来出现在端子之间。
这也与转速成正比,因此,使用反电动势常数KE来表述。
e = KEω ……(2.7)
e:这里,出现在马达端子上的发生电压(反电动势常数换算)[V]
KE:反电动势常数[Vs/rad]
ω:转速[rad/s]
通过实际马达测量这种关系,则变成图2.8 所示的直线。
实际上,反电动势常数KE和扭矩常数KT是同一常数,参见以下证明。
假设线圈圈数为N,则发生电压e与反电动势常数KE之间的关系如下。
e = 2RNBLω = KEω ……(2.8)
这里,在(2.7)公式中代入(2.4)公式中的KT=2RNBL,则两边除以ω,则变成
KT = KE ……(2.9)
直流马达中,KT和KE相同,是什么意思呢?
简单来说,所谓马达,是指电气-机械之间的双向能量转换器。
那么,可解释为从“电气→机械”的方向看能量转换,则为弗莱明左手法则,其转换系数为KT。
另一方面,从“机械→电气”的方向看则为弗莱明右手法则,其转换系数变成KE。这样,KT和KE是同一系数,但本书为了明确转换方向,今后也会将KT和KE分开使用。
观察马达的发电作用
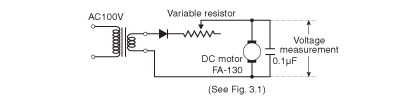
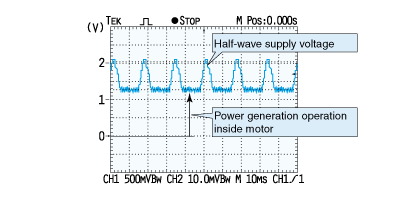
发电作用在电流流向马达,进行旋转时也会发生。为了观察这种现象,如图2.9 所示,利用二极管对降压后的交流进行半波整流后形成电源,使用该电源来旋转之前的马达。
虽然输入为正弦波的一半,但观察马达端子间电压,则可以观测到图2.10 所示的波形。这就是因马达内部发电作用而产生的(2.7)公式中的电压(反电动势常数换算)。
电压平衡
图2.11 表示发电作用在马达内部发挥的功能。图中,针对外部电压v,基于线圈电阻Ra的电压下降RaIa、电刷接触部的电压下降VB及基于马达旋转的内部发电电压(反电动势常数换算)e=KEω之和处于平衡状态。
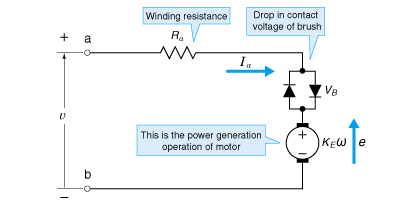
那么,外部电压变高的话,会发生什么变化呢?
- ①线圈电阻Ra两端的电压差变大,电路电流Ia增大
- ②电流增加,则扭矩增大
- ③扭矩增大导致马达加速,旋转加快
- ④旋转加快,则反电动势常数换算增大
按这样的顺序,在达到新的稳定状态之前,转速会升高。
接着,电压在固定状态下,外部负载增大后,会如何?
- ①转速下降后,反电动势常数换算也会下降
- ②其结果是,线圈电阻部会产生电压差,电流增大
- ③电流增大后,马达的扭矩变大,与外部负载平衡
现在,马达以低于之前的速度,趋于稳定。
直流马达具有,
- ・负载相同,增大电压,则速度会上升
- ・负载增加后,转速下降,扭矩增大
的性质。也就是说,以前认为存在于其它产品中基于左手法则和右手法则的作用也同时存在于马达中,两者相互平衡,共同决定马达的转速。
转速与扭矩的关系
以曲线的方式表示直流马达的转速和扭矩之间的关系,则得出图 2.12 的曲线图。
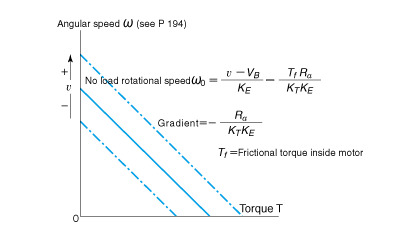
供电电压固定时,直流马达的特性如该曲线所示,变成自左向右下降的直线。
直线的左上角为无负载时的角速度,右下角为启动时的扭矩。此外,供电电压增高,则直线会朝右上方平行移动,电压下降,则朝左下方平行移动。
在之前的直流马达中,可以得知扭矩与电流成正比增加的性质。而此次我们可以知道增大电压后,转速会上升的性质。这是对于控制来说非常实用的性质。
还有一个需要关注的性质是,直流马达基于T=KT(2.3式)的关系,即使是速度为零时,也会发生与电流成正比的扭矩。这表示在定位控制中,即使施加了较大的外力,也能够控制电流,保持停止位置。
这是感应马达及步进马达所不具有,而只有直流马达及无刷直流马达才具有的性质。这些马达用于伺服控制就是因为它们具有能够保持停止位置的性质。
<小知识> N-T特性
有时会将转速单位设成[rpm],将表示其与扭矩之间关系的特性称为N-T特性。
无铁芯的马达实例
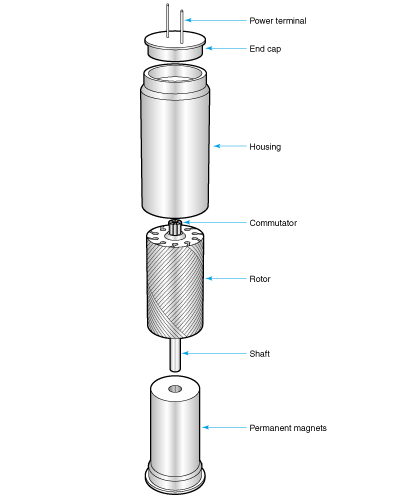
前面介绍的最接近无铁芯马达的实用马达是空心马达或称为动圈马达的马达。
空心马达,就像名称那样,转子不使用铁芯,使用树脂加固后的线圈作为转子使用的马达。其例子见图2.13 ,截面图见图2.14 。
空心马达也包括线圈为平板形状的马达。这种马达的制作方法与印刷电路板的制作方法相同,因此,也称为打印马达。
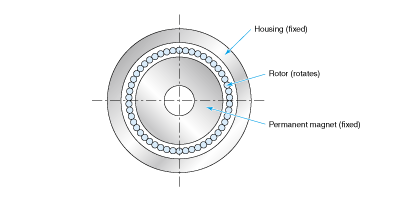
转子不使用铁,会有以下多种优点。
- ●惯性力矩小,动作敏捷(*注)
- ●磁铁的吸力不会作用到转子上,旋转顺畅
- ●感应低,整流时不易产生火花
- ●不易产生火花,电刷磨耗小
- ●磨耗小,则可使用金属刷,接触电压下降程度会减少,马达效率变高
也有缺点。
- ●由于小型化及高性能化,需使用铝镍钴磁铁及稀土类磁铁等昂贵的磁铁
- ●线圈的制造成本升高
- ●使用贵金属刷及贵金属整流子,致使制造成本升高
空心马达因量少价高,很难成为直流马达的主流,一直用于小型设备、检测设备或精密控制用马达。
但,近年来,它发挥了小型马达的长处,作为手机的振动马达(pager motor)使用,已成为身边常见的一种马达。
虽然不是空心马达,但仍是在圆筒状铁芯上缠绕了线圈的马达。该马达与普通的直流马达相比,由于铁芯没有切槽,因此,称为无槽式马达。
无槽马达的铁芯与线圈一起旋转,其工作原理与空心马达几乎相同。无槽马达在无刷直流马达出现之前一直是高性能控制用马达。
- *注:打印马达的线圈呈扁平状,因此,惯性力矩(moment of inertia)并不小
