2-1-2 旋转原理的基础知识
2-1节的最终目标是了解我们所熟悉的,有铁芯的直流马达的旋转原理。
但,这需要具备与马达相关的基础知识。
因此,首先像理科及物理教科书一样,思考一下转子没有铁芯的马达。
同时,对于没有铁芯的马达,不仅仅是理论,还应确认一下作为马达已实用化的情况。
虽说是这样,但我们的目的是“让繁杂技术浅显化”。不仅仅是复习,也做一些对实务有用的探讨。
BLI法则
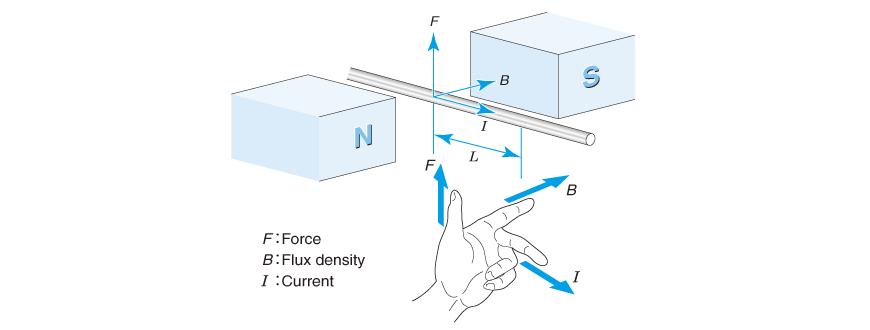
如图2.2 所示,空中有一个磁场B,对横穿磁场的电线上通电,则电线上会产生力F。该力的强度可通过下面的公式计算,也称为BLI法则。
F = BLⅠ ……(2.1)
F:力[N] B:磁束密度[T]
L:磁场中的电线长度[m] Ⅰ:电流[A]
此外,作用到电线上的力的方向,因弗莱明左手法则,变成图中的方向。
手指与记号之间的对应关系,记住从母指开始依次为“F・B・Ⅰ”,从中指开始按相反的顺序依次为“电・磁・力”。
记号B表示磁力线的强度,称为磁束密度。磁力线是想像的物质,无法直接进行确认。磁束密度的国际单位(SI)是T(特斯拉),与MKS单位的[Wb/m2]相同。
所谓1特斯拉,是指一平方米中存在1韦伯[Wb]磁通时磁场的强度。
物理学者及磁铁生产厂家还使用另外一个单位,高斯[G]。1T等于10,000G。
无铁芯的马达旋转原理
如图2.3 所示,将电线制成线圈,按图示方向通入电流I,则线圈的左侧、右侧会分别产生朝上、朝下的力,线圈开始旋转。这就是在学校中学到的直流马达的旋转原理。
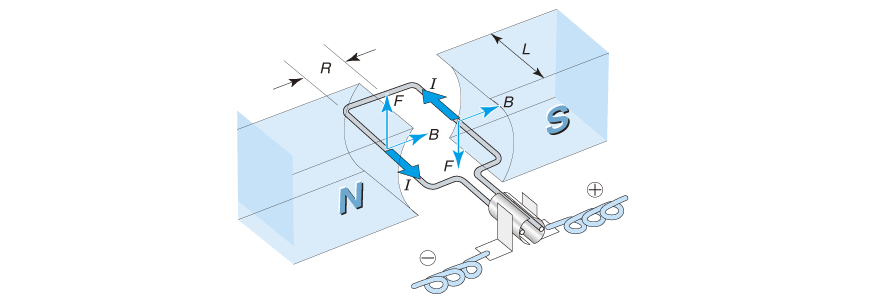
T =2RF = 2RNBLⅠ ……(2.2)
T:扭矩[Nm] R:旋转半径[m] N:线圈圈数
L:磁通宽[m]
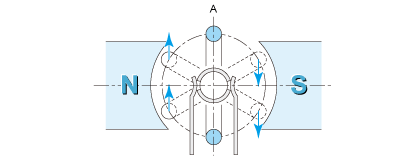
但,在线圈为一组时,当线圈到达图2.4 中A位置时,无法决定朝哪个方向旋转。 因此,使用多组线圈,根据旋转情况依次切换电流,则线圈群会连续旋转。
首先思考一下只有1个线圈的马达。基于公式(2.2),考虑磁通分布、线圈半径和长度、电流的流动方向,则此时的扭矩T(torque)与电流I成正比,可使用下面的公式进行表述。这种比例系数KT称为扭矩常数。
T = KTI ……(2.3)
I:线圈电流[A] KT:扭矩常数[Nm/A]
在直流马达中,该公式表示扭矩与电流成正比。这是直流马达所具有的极其重要的性质之一。
扭矩常数根据(2.2)公式和(2.3)公式,变成下面的公式。
KT= 2RNBL[Nm/A] ……(2.4)
实际的马达中,如后面介绍的图2.16 所示,有多个线圈,像花瓣那样进行连接,马达端子的电流流动时将马达内部分成2部分。这里,将所有线圈的圈数取N,则扭矩常数即(2.4)公式。

制作Clip马达
下面我们将制作一下中学教科书中的一种简单马达,Clip马达。
材料可到文具商店及建材商店购买。
制作方法,请参考图2.5 。缠绕珐琅线,制作线圈。
珐琅线最好是粗0.4~0.6mm,圈数约15~30圈。使用矿泉水瓶的盖子缠绕线圈会非常合适。缠绕后,将线圈调整成尽可能与旋转轴对称。
剥除线圈端部的外皮时要细心。一头全部剥去,但另一头只剥一半,注意看放大图。这是Clip马达的制作要点。
还要注意剥离的范围以及与线圈之间的角度。
将线圈插入别针,朝任何一个方向轻轻转动,都能够不停旋转。
如果线圈呈对称状态,则也会朝反方向旋转,但如果不对称,则只能朝一个方向旋转。
缠绕粗0.4~0.6mm的漆包线15~30圈
将包漆全部剥开只剥一半包漆
将别针插到橡皮上